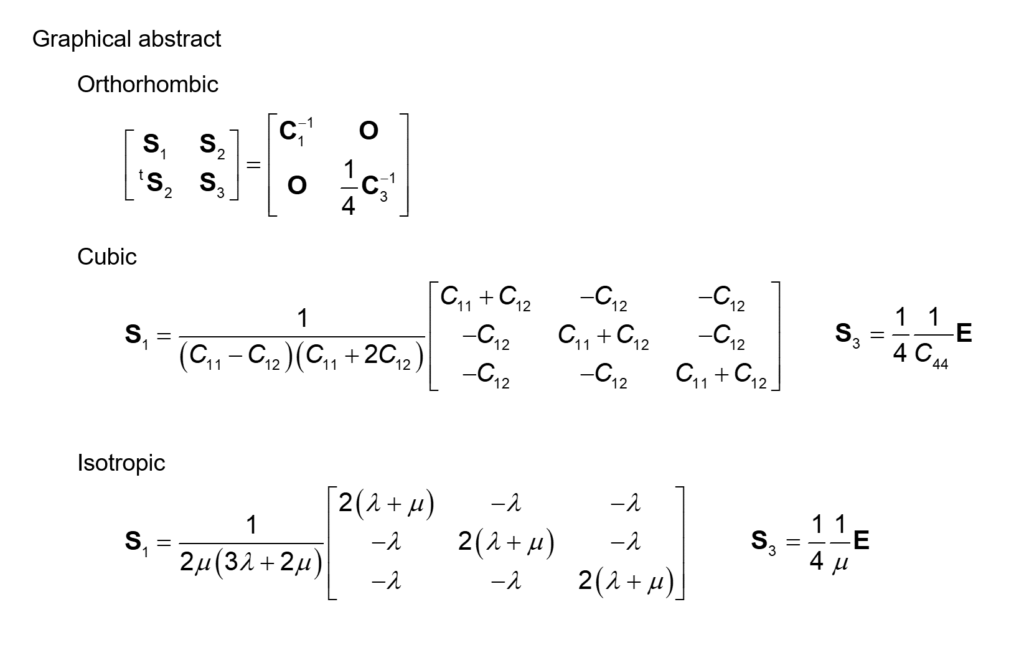
本記事では、直方晶、立方晶、等方弾性体について、弾性定数コンプライアンスを示します。
Webページ上では要点のみを示しますので、細かな式展開については本ページ下部のpdfファイルをご確認ください。
なお、直方晶、正方晶、等方弾性体の弾性スティフネスについては、以下の記事をご確認ください。

直方晶
Voigt表記(フォークト表記: Voigt notation)を用いて、弾性スティフネス(Elastic stiffness)\(\mathbf{C}\)と弾性コンプライアンス( Elastic compliance)\(\mathbf{S}\)を6×6の行列として記述します。
弾性スティフネス
$$
\mathbf{C}=
\left[
\begin{array}{cc}
\mathbf{C}_1 & \mathbf{C}_2 \\
^{\mathbf{t}} \! \mathbf{C}_2 & \mathbf{C}_3 \\
\end{array}
\right]
=
\left[
\begin{array}{ccc}
C_{1111} & C_{1122} & C_{3311} & C_{1123} & C_{1131} & C_{1112} \\
C_{1122} & C_{2222} & C_{2233} & C_{2223} & C_{2231} & C_{2212} \\
C_{3311} & C_{2233} & C_{3333} & C_{3323} & C_{3331} & C_{3312} \\
C_{1123} & C_{2223} & C_{3323} & C_{2323} & C_{2331} & C_{2312} \\
C_{1131} & C_{2231} & C_{3331} & C_{2323} & C_{2331} & C_{2312} \\
C_{1112} & C_{2212} & C_{3312} & C_{2312} & C_{3112} & C_{1212} \\
\end{array}
\right]
\tag{1}
$$
弾性コンプライアンス
$$
\mathbf{S}=
\left[
\begin{array}{cc}
\mathbf{S}_1 & \mathbf{S}_2 \\
^{\mathbf{t}} \! \mathbf{S}_2 & \mathbf{S}_3 \\
\end{array}
\right]
=
\left[
\begin{array}{cccccc}
S_{1111} & S_{1122} & S_{3311} & S_{1123} & S_{1131} & S_{1112} \\
S_{1122} & S_{2222} & S_{2233} & S_{2223} & S_{2231} & S_{2212} \\
S_{3311} & S_{2233} & S_{3333} & S_{3323} & S_{3331} & S_{3312} \\
S_{1123} & S_{2223} & S_{3323} & S_{2323} & S_{2331} & S_{2312} \\
S_{1131} & S_{2231} & S_{3331} & S_{2323} & S_{2331} & S_{2312} \\
S_{1112} & S_{2212} & S_{3312} & S_{2312} & S_{3112} & S_{1212} \\
\end{array}
\right]
\tag{2}
$$
\(\mathbf{S}\)と\(\mathbf{C}\)の間には以下の関係が成立します。
\(\mathbf{S}\)と\(\mathbf{C}\)の関係式
$$ \mathbf{S}_1= \left( \mathbf{C}_1-\mathbf{C}_2 \mathbf{C}_3^{-1} {}^{\mathrm{t}} \! \mathbf{C}_2 \right) ^{-1} \tag{3} $$
$$ \mathbf{S}_3= \frac{1}{4} \left( \mathbf{C}_3 – {}^{\mathrm{t}} \! \mathbf{C}_2 \mathbf{C}_1^{-1} \mathbf{C}_2 \right) ^{-1} \tag{4} $$
$$ \mathbf{S}_2= -\frac{1}{2} \mathbf{S}_1 \mathbf{C}_2 \mathbf{C}_3^{-1} = -2 \mathbf{C}_1^{-1} \mathbf{C}_2 \mathbf{S}_3 \tag{5} $$

直方晶系の\(\mathbf{C}\)をEqs. (3)~(5)に代入すると\(\mathbf{S}\)が得られます。
直方晶の\(\mathbf{C}\)
$$
\mathbf{C}_1=
\left[
\begin{array}{ccc}
C_{11} & C_{12} & C_{31} \\
C_{12} & C_{22} & C_{23} \\
C_{31} & C_{23} & C_{33} \\
\end{array}
\right]
\tag{1-1} $$
$$ \mathbf{C}_2=\mathbf{O} \tag{1-2} $$
$$
\mathbf{C}_3=
\left[
\begin{array}{ccc}
C_{44} & 0 & 0 \\
0 & C_{55} & 0 \\
0 & 0 & C_{66} \\
\end{array}
\right]
\tag{1-3} $$

$$ \mathbf{S}_1=\mathbf{C}_1^{-1} \tag{1-4} $$
$$ \mathbf{S}_3=\frac{1}{4}\mathbf{C}_3^{-1} \tag{1-5} $$
$$ \mathbf{S}_2=\mathbf{O} \tag{1-6} $$
立方晶
立方晶(Cubic)の\(\mathbf{C}\)をEqs. (3)~(5)に代入すると\(\mathbf{S}\)が得られます。
立方晶の\(\mathbf{C}\)
$$
\mathbf{C}_1=
\left[
\begin{array}{ccc}
C_{11} & C_{12} & C_{12} \\
C_{12} & C_{11} & C_{12} \\
C_{12} & C_{12} & C_{11} \\
\end{array}
\right]
\tag{2-1} $$
$$ \mathbf{C}_2=\mathbf{O} \tag{2-2} $$
$$ \mathbf{C}_3=C_{44} \mathbf{E} \tag{2-3} $$

$$
\mathbf{S}_1=
\frac{1}{ \left( C_{11}-C_{12} \right) \left( C_{11}+2C_{12} \right) }
\left[
\begin{array}{ccc}
C_{11}+C_{12} & -C_{12} & -C_{12} \\
-C_{12} & C_{11}+C_{12} & -C_{12} \\
-C_{12} & -C_{12} & C_{11}+C_{12} \\
\end{array}
\right]
\tag{2-4} $$
$$ \mathbf{S}_3=\frac{1}{4} \frac{1}{C_{44}} \mathbf{E} \tag{2-5} $$
$$ \mathbf{S}_2=\mathbf{O} \tag{2-6} $$
ここで、\(\mathbf{E}\)は単位行列です。
等方弾性体
等方弾性体の\(\mathbf{C}\)は、Eqs. (2-1)~(2-3)と以下の式で与えられます。これを、Eqs. (3)~(5)に代入すると\(\mathbf{S}\)が得られます。
等方弾性体の\(\mathbf{C}\)
$$ C_{11}=\lambda +2 \mu \tag{3-1} $$
$$ C_{12}=\lambda \tag{3-2} $$
$$ C_{44}=\mu \tag{3-3} $$

$$
\mathbf{S}_1=
\frac{1}{ 2 \mu \left( 3 \lambda + 2 \mu \right) }
\left[
\begin{array}{ccc}
2 \left( \lambda + \mu \right) & -\lambda & -\lambda \\
-\lambda & 2 \left( \lambda + \mu \right) & -\lambda \\
-\lambda & -\lambda & 2 \left( \lambda + \mu \right) \\
\end{array}
\right]
\tag{3-4} $$
$$ \mathbf{S}_3=\frac{1}{4} \frac{1}{\mu} \mathbf{E} \tag{3-5} $$
$$ \mathbf{S}_2=\mathbf{O} \tag{3-6} $$
ここで、\(\lambda, \mu \)はラメ定数です。
詳細な式展開(PDFファイル)
関連ページ
弾性コンプライアンスと弾性スティフネスの関係

直方晶・正方晶・立方晶・等方弾性体の弾性スティフネス

弾性定数の対称性(基本的な対称性)

六方晶の弾性スティフネス

