真応力・真ひずみと公称応力・公称ひずみ

2021年6月15日2024年11月23日

本記事では、一軸引張試験における、真応力と真ひずみ、公称応力と公称ひずみについて解説します。

引張試験は、所定の形状に加工した試験片を特定の方向に引張るという非常にシンプルな試験で、金属材料の力学特性を調べるための基本的な試験の一つです。

測定データとしては伸び（変形量）と荷重が得られ、これらを整理することで応力‐ひずみ（S-S: stress-strain）曲線が得られます。

この応力とひずみには、それぞれ真応力と真ひずみ、公称応力と公称ひずみの2種が存在し、S-S曲線にも、真応力‐真ひずみ曲線と、公称応力‐公称ひずみ曲線が存在します。

引張試験の結果を正しく活用するためには、これら2種の応力とひずみを正しく理解することが不可欠です。

本稿では、これら2種の応力とひずみについて解説します。

また、均一変形範囲内で成立する、真応力・真ひずみと公称応力・公称ひずみの換算式についても紹介します。

本記事の関連分野

専門：材料力学、引張試験

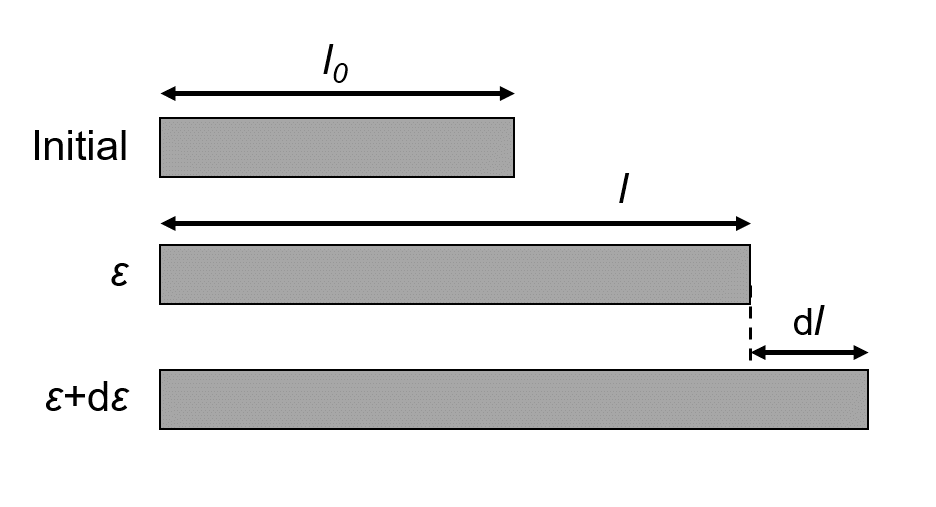
引張変形の模式図と変数の定義

本稿では、以下のような引張変形を考えます。

まず、断面積\(A_0\)（試験片全体で一定）、長さ\(l_0\)の試験片を、下図のように長さ\(l\)になるまで引張ります。

この時の試験片断面積を\(A\)、荷重を\(F\)、ひずみを\(\varepsilon\)とします。

さらに、ここから微量だけ引張り、長さを微小量\(\mathrm{d}l\)だけ増加させたときの、微小ひずみ増分\(\mathrm{d}\varepsilon\)を考えます。

真応力と真ひずみ

真応力\(\sigma^{\mathrm{t}}\)と真ひずみ\(\varepsilon^{\mathrm{t}}\)はその名の通り、この材料の変形に関わる真の応力とひずみで、下式により表現されます。

\[ \sigma^{\mathrm{t}}=\frac{F}{A} \tag{1} \]

\[ \mathrm{d}\varepsilon^{\mathrm{t}}=\frac{\mathrm{d}l}{l} \tag{2} \]

\(\varepsilon^{\mathrm{t}}\)は、Eq. (2)を積分することで得ることができます。

\[
\begin{eqnarray}
\varepsilon^{\mathrm{t}}
&=&\int_{l_0}^{l} \frac{\mathrm{d}l}{l}=\left[ \ln l \right]_{l_0}^l \\
&=& \ln l- \ln l_0=\ln \left( \frac{l}{l_0} \right)
\end{eqnarray}
\]

つまり、\(\sigma^{\mathrm{t}}\)と\(\varepsilon^{\mathrm{t}}\)はそれぞれ下式で表されます。

真応力: \[ \sigma^{\mathrm{t}}=\frac{F}{A} \tag{1} \]
真ひずみ: \[ \varepsilon^{\mathrm{t}}=\ln \left( \frac{l}{l_0} \right) \tag{3} \]

このように、真ひずみは、対数で表されるため、対数ひずみとも呼ばれます。

公称応力と公称ひずみ

先に述べたように真応力と真ひずみは、材料の変形に関わる真の応力とひずみであるため、本来、材料の変形は真応力と真ひずみで議論されるべきです。

しかし、真応力を計算するためには、Eq. (1)に示すように変形中の断面積（\(A\)）が必要となります。

\(A\)は、後述する均一変形範囲内であれば、体積一定の条件から求めることができますが、引張試験の後半では局所変形が生じるため、\(A\)を求める事は容易ではありません。

また、不均一変形中は、試験片の長手方向に\(l\)ならびに\(\mathrm{d}l\)の分布も生じるため、真ひずみを求めることも簡単ではありません。

そこで、便宜的に用いられのが、公称応力\(\sigma^{\mathrm{n}}\)と公称ひずみ\(\varepsilon^{\mathrm{n}}\)です。

これらは下式で表現されます。

\[ \sigma^{\mathrm{n}}=\frac{F}{A_0} \tag{4} \]

\[ \mathrm{d}\varepsilon^{\mathrm{n}}=\frac{\mathrm{d}l}{l_0} \tag{5} \]

\(\varepsilon^{\mathrm{n}}\)は、Eq. (5)を積分することで得ることができます。

\[
\begin{eqnarray}
\varepsilon^{\mathrm{t}}
&=&\int_{l_0}^{l} \frac{\mathrm{d}l}{l_0}=\frac{1}{l_0} \left[ l \right]_{l_0}^l \\
&=& \frac{l-l_0}{l_0}
\end{eqnarray}
\]

つまり、\(\sigma^{\mathrm{n}}\)と\(\varepsilon^{\mathrm{n}}\)はそれぞれ下式で表されます。

公称応力: \[ \sigma^{\mathrm{n}}=\frac{F}{A_0} \tag{4} \]
公称ひずみ: \[ \varepsilon^{\mathrm{n}}= \frac{l-l_0}{l_0} \tag{6} \]

このように、公称応力、公称ひずみは、初期状態を基準とするため、不均一変形範囲でも計算可能です。

そのため、これらを用いることで、不均一変形の開始から破断までの範囲を取り扱うことができる利点があります。

しかし、公称応力、公称ひずみはあくまでも便宜的な値であり、材料中の本当の応力ならびにひずみではない点には注意が必要です。

真応力・真ひずみと公称応力・公称ひずみの換算式

均一変形範囲内であれば、真応力、真ひずみと公称応力、公称ひずみを相互に換算することができます。

均一変形中は、\(A\)が試験片全体で一定となるので、変形中の試験片の体積を\(Al\)で表すことができます。

塑性変形中は体積が一定となるため、下式が成立します。

\[ Al=A_0 l_0 \tag{7} \]

これらを用いて、Eq. (1)を変形すると、以下のようになります。

Eq. (7)を代入: \[ \sigma^{\mathrm{t}}=\frac{F}{A_0}\frac{l}{l_0} \]
式を整理: \[ \sigma^{\mathrm{t}}=\frac{F}{A_0}\frac{l-l_0+l_0}{l_0}=\frac{F}{A_0} \left( \frac{l-l_0}{l_0}+1\right) \]
Eqs. (4), (6)を代入: \[ \sigma^{\mathrm{t}}=\sigma^{\mathrm{n}} \left( \varepsilon^{\mathrm{n}}+1\right) \]

続いて、Eq. (3)を変形すると、以下のようになります。

式を整理: \[ \varepsilon^{\mathrm{t}}=\ln \left( \frac{l}{l_0} \right)=\ln \left( \frac{l-l_0+l_0}{l_0} \right)=\ln \left( \frac{l-l_0}{l_0}+1 \right) \]
Eq. (6)を代入: \[ \varepsilon^{\mathrm{t}}=\ln \left( \varepsilon^{\mathrm{n}}+1 \right) \]

逆にこれらの式から以下の式が成立します。

\[ \varepsilon^{\mathrm{n}}=\exp \left( \varepsilon^{\mathrm{t}} \right) -1 \]

\[ \sigma^{\mathrm{n}}=\frac{ \sigma^{\mathrm{t}} }{ \exp \left( \varepsilon^{\mathrm{t}} \right) } \]

つまり整理すると、以下の換算式が成立します。

真応力: \[ \sigma^{\mathrm{t}}=\sigma^{\mathrm{n}} \left( \varepsilon^{\mathrm{n}}+1\right) \tag{8}\]
真ひずみ: \[ \varepsilon^{\mathrm{t}}=\ln \left( \varepsilon^{\mathrm{n}}+1 \right) \tag{9}\]
公称応力: \[ \sigma^{\mathrm{n}}=\frac{ \sigma^{\mathrm{t}} }{ \exp \left( \varepsilon^{\mathrm{t}} \right) } \tag{10}\]
公称ひずみ: \[ \varepsilon^{\mathrm{n}}=\exp \left( \varepsilon^{\mathrm{t}} \right) -1 \tag{11}\]