N分の1で当たるくじに関する確率

本記事では、N分の1で当たるくじに関する確率について、数式を用いて解説します。

100分の1の確率（1%）で当たるくじがあるとします。

感覚的には、このくじを100回引けば当たるが出るような気がしますが、実際には1回も当たるが出ないこともあります。

では、このくじを100回引いたときに少なくとも1回当たるが出る確率はどの程度なのでしょうか。

本稿では、一般化した\(N\)回に1回あたるくじに関する確率について解説します。

\(N\)回くじを引いて、少なくとも1回は当たる確率\(P(N)\)

\(N\)分の1の確率で当たるくじを\(N\) 回引いたときに少なくとも1回当たる確率を\(P(N)\)とします。

\(P(N)\)は、余事象（全てはずれる場合）を考えることで容易に計算できます。

各くじが外れる確率は\((N-1)/N\)となるので、\(N\)回外れる確率\(1-P(N)\)は下式で与えられます。

\[ 1-P(N)= \left( \frac{N-1}{N} \right) ^N \tag{1} \]

つまり、\(P(N)\)は以下のようになります。

\[ P(N)= 1- \left( \frac{N-1}{N} \right) ^N \tag{2} \]

Eq. (2)を具体的に計算すると下表のようになります。

\(N\)	1	2	3	4	5	10	100	1000
\(P(N)\) (%)	100	75	70.4	68.4	67.2	65.1	63.4	63.2

冒頭例に挙げた、100分の1の確率（1%）であたるくじであれば、\(P(100) \approx \)63%となります。

つまり、100回引いた場合にあたりが出る確率は2/3（約67%）以下となります。

逆に言えば、100回引いても、1/3以上の確率で全て外れることとなります。

\(N\)と\(P(N)\)の関係

Eq. (2)より、\(P(N)\)を\(N\)に対してプロットすると、下図のようになります。

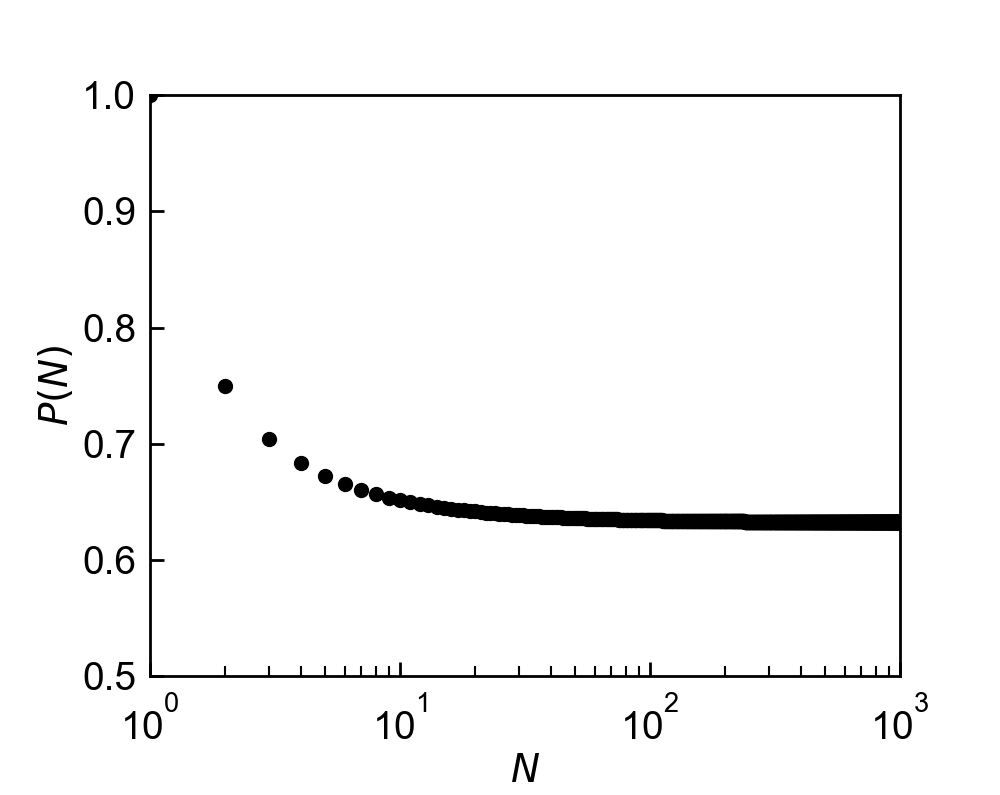
この図から、\(P(N)\)は、\(N\)の増加に伴って減少し、一定値に収束することが分かります。

この収束値は、\( N \to \infty\)の極限を考えることで知る事ができます。

\[ \lim_{N \to \infty} P(N)= \lim_{N \to \infty} \left\{ 1- \left( \frac{N-1}{N} \right) ^N \right\} \]

第2項について、以下のEq. (3)が成立するので、これを代入するとEq. (4)が得られます。

\[ \lim_{N \to \infty} P(N)= 1- \frac{1}{e} \tag{4} \]

この値を数値計算すると、\(P(\infty) \approx \)63%となります。

これらの結果から、63% \( < P(N) \leq \) 75%となることが分かります（\(N\)=1の場合は全て当たりで実用的に意味がないので、\(N \geq \)2を考えています）。

逆に言えば、25%（=1/4）～37％（\(\approx 1/e\)）の確率で、全てのくじが外れることになります。

1回当たりを引くのに必要なくじ引きの回数の期待値

上記の計算結果はいかがだったでしょうか？

直感に反して、\( P(N) \)が低く、全て外れる確率が高いと感じた方も多いのではないでしょうか？

続いて、1回あたりを引くために必要なくじ引きの回数の期待値\(N_{\mathrm{E}}\)について考えてみます。

まず、\(N\)分の1の確率で当たるくじを、\(M\)回引いて\(M\)回目に当たる確率を\(P^{\mathrm{f}}(N,M)\)とします。

ここで、下式が成立します。

\[ N_{\mathrm{E}}=\sum_{M=1}^{\infty} MP^{\mathrm{f}}(N,M) \tag{5}\]

\(P^{\mathrm{f}}(N,M)\)は、先に\(M-1\)回外れを引いて最後に1回あたりを引く確率なので、下式で表すことができます。

\[ P^{\mathrm{f}}(N,M) = \left( \frac{N-1}{N} \right) ^{M-1} \frac{1}{N} \tag{6} \]

これらを用いると、\(N_{\mathrm{E}}\)を以下のように計算することができます。

Eq.（6)を代入して整理

\[ N_{\mathrm{E}}=\frac{1}{N}\sum_{M=1}^{\infty} M \left( \frac{N-1}{N} \right) ^{M-1} \]

以下の関係式を用いて整理

関係式

\[ \frac{1}{N}\sum_{M=1}^{\infty} M \left( \frac{N-1}{N} \right) ^{M-1}=N \]

本関係式の導出は本ページ下部のpdfファイルを参照してください。

\[ N_{\mathrm{E}}=N \tag{7}\]

Eq. (7)は、平均\(N\)回くじを引けばあたりが出る事を意味しています。

一見、この結果は、先の結果（\( P(N) \)）と矛盾しているようにも感じるかと思いますが、どちらも正しい結論です。

では、なぜこのような齟齬が生じるのでしょうか？

それは、\( P(N) \)の計算では、複数回当たりが出るという事象が評価されていない事に起因しています。

例えば、\(N=100\)では、前述の通り100回くじを引いても1/3程度は全て外れることになりますが、その分2回以上当たりが出る場合もあり、全体では帳尻が合っています。

詳細な式展開（PDFファイル）

以下のpdfファイルより、本記事に関係する式展開の詳細をご確認頂けます。

適宜ご参照ください。