金属材料に対して一軸引張試験を行うと、途中でくびれが発生し、最終的には局所変形の進行によって破断に至ります。局所的な変形が発生すると、その領域だけ断面積が減少し、作用する応力が上昇するため、変形が集中しやすくなります。このページでは、何らかのよう要因によって、局所的な変形が生じた場合に、その領域での変形が集中的に進行するための条件についてまとめます。各関係式の導出過程は以下のPDFファイルをご確認ください。
本ページでは、以下の記事で紹介した引張試験中のくびれの発生条件を、別の考え方から導いたものに相当します。適宜、以下の記事もご確認ください。
状況設定・記号の定義
状況設定
下図のように、ハッチングした長さ\(h\)の領域が、何らかの要因によって局所的に微小長さ\(\mathrm{d} h\)だけ変形した場合を考え、この領域において変形が進行するための条件をまとめます。
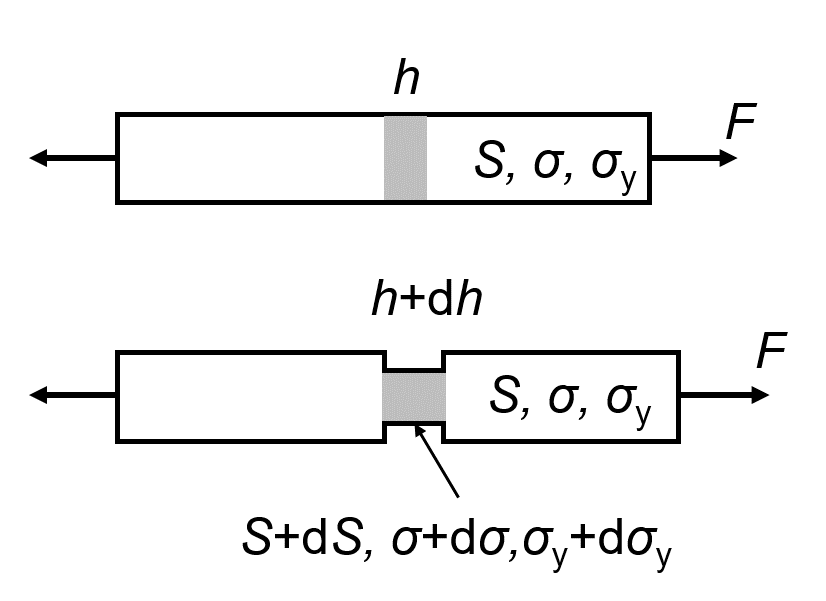
記号の定義
\(F\): 外力(Force)
\(S\): 非局所変形領域の断面積
\(\sigma\): 非局所変形領域に作用する真応力
\(\sigma_{\mathrm{y}}\): 非局所変形領域の塑性変形に必要な真応力
\(h\): 局所変形前の変形領域の長さ
\(h+\mathrm{d} h \): 局所変形後の変形領域の長さ
\(\sigma+ \mathrm{d} \sigma \): 局所変形領域に作用する真応力
\(\sigma_{\mathrm{y}}+ \mathrm{d} \sigma_{\mathrm{y}} \): 局所変形領域の塑性変形に必要な真応力
\(\mathrm{d} \varepsilon\): 局所変形による真ひずみ
局所変形の進行条件
一連の関係式の導出過程については、本ページ上部のpdfファイルをご確認ください。
断面積の減少による応力増加
外力一定の場合、局所的な変形による断面積の減少によって増加する、応力\(\mathrm{d} \sigma\)は以下の式で与えられます。
$$ \mathrm{d} \sigma=\sigma \mathrm{d} \varepsilon \tag{1} $$
加工硬化
一方、この領域では塑性変形が進行するので、下図のように塑性変形に必要な応力も増加し、その増分は以下の式で与えられます。
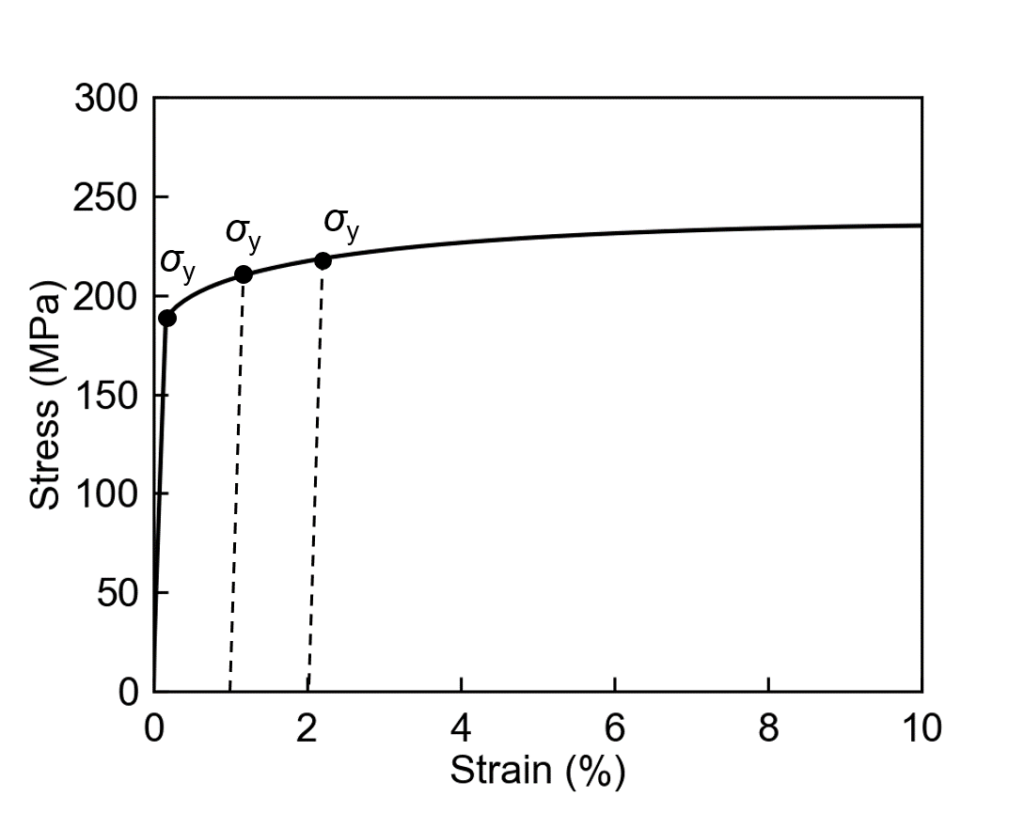
$$ \mathrm{d} \sigma_{\mathrm{y}}= \frac{\mathrm{d} \sigma_{\mathrm{y}}}{\mathrm{d} \varepsilon} \mathrm{d} \varepsilon \tag{2} $$
\(\mathrm{d} \sigma_{\mathrm{y}} / \mathrm{d} \varepsilon\)は 、応力-ひずみ曲線の傾きに相当します。
局所変形の進行条件
ここで、\( \mathrm{d} \sigma\)が\( \mathrm{d} \sigma_{\mathrm{y}} \)よりも大きければ、外力が増加せずとも局所変形領域で塑性変形が進行することになります。つまり、局所変形の進行条件は、
$$ \mathrm{d} \sigma_{\mathrm{y}}< \mathrm{d} \sigma \tag{3} $$
$$ \sigma > \frac{\mathrm{d} \sigma_{\mathrm{y}}}{\mathrm{d} \varepsilon} \tag{4} $$
となります。
逆に局所変形が進行しない場合を考えると、
$$ \sigma = \sigma_{\mathrm{y}} \tag{5} $$
が成立しているので、 局所変形が進行しない条件はEqs. (4, 5)より、以下のようになります。
$$ \sigma < \frac{\mathrm{d} \sigma_{\mathrm{y}}}{\mathrm{d} \varepsilon} \tag{6} $$
$$ \sigma _{\mathrm{y}} < \frac{\mathrm{d} \sigma_{\mathrm{y}}}{\mathrm{d} \varepsilon} \tag{7} $$
Eqs. (4, 7)より連続性を加味して、局所変形が進行するための開始条件を考えると、以下の関係式が得られます。
$$ \sigma _{\mathrm{y}} = \frac{\mathrm{d} \sigma_{\mathrm{y}}}{\mathrm{d} \varepsilon} \tag{8} $$
この式は、以下の記事で紹介した”くびれの発生条件”(Eq. (3))に対応しています。本記事では、S-S曲線に対応した真応力を\( \sigma_{\mathrm{y}} \)としている点に注意してください。
局所変形中の進行条件
上記の議論は、何等かの要因で微小局所変形が生じた場合を想定しているため、Eq. (4)は局所変形の開始直後にしか適用できません。局所変形中に変形が進行するための条件は、局所変形領域に作用する局所応力\(\sigma_{\mathrm{L}}\)と局所ひずみ\(\varepsilon_{\mathrm{L}}\)を用いることで以下のように記述できます。詳細な導出過程は本ページ上部のpdfファイルをご確認ください。
$$ \sigma_{\mathrm{L}}> \frac{\mathrm{d} \sigma_{\mathrm{L}} }{\mathrm{d} \varepsilon_{\mathrm{L}} } \tag{9} $$
また、外力を考えると局所変形の開始条件として、
$$ \mathrm{d} F=0 \tag{10}$$
が得られ、局所変形の開始時に外力が極大となります。この式は、以下の記事で紹介した”くびれの発生条件”(Eq. (1))に対応しています。
局所変形が進行しない条件での変形
Eq. (7)の条件が成立している場合、試験片の変形が進行するためには外力の増加が必要です。外力が\(\Delta F\)だけ増加したときの、 非局所変形部と局所変形部に作用する応力は以下のようになります。
非局所変形部
$$ \sigma_{\mathrm{y}}+\frac{\Delta F}{S} \tag{2-1}$$
局所変形部
$$ \sigma_{\mathrm{y}}+\mathrm{d} \sigma_{\mathrm{y}}-\delta +\frac{\Delta F}{S+\mathrm{d} S} \tag{2-2}$$
ここで、
$$ \mathrm{d} \sigma=\mathrm{d} \sigma_{\mathrm{y}}-\delta \tag{2-3}$$
であり、Eq. (6)より、
$$ \delta>0 \tag{2-4}$$
である。
\(\delta\)は\(\Delta F\)と無関係であるため、 \(\Delta F\)が十分に小さければ、Eqs. (2-1, 2-2)より、非局所変形部においてのみ塑性変形が進行する。
つまり、十分な加工硬化が生じる条件では、何らかの要因によって局所的な変形が生じても、加工硬化による硬化能が大きく、先に周辺領域の塑性変形が生じるため、局所変形は進行しない。

