本記事では、対数関数の微分について導出過程を示します。
高校数学:指数関数、対数関数、微分
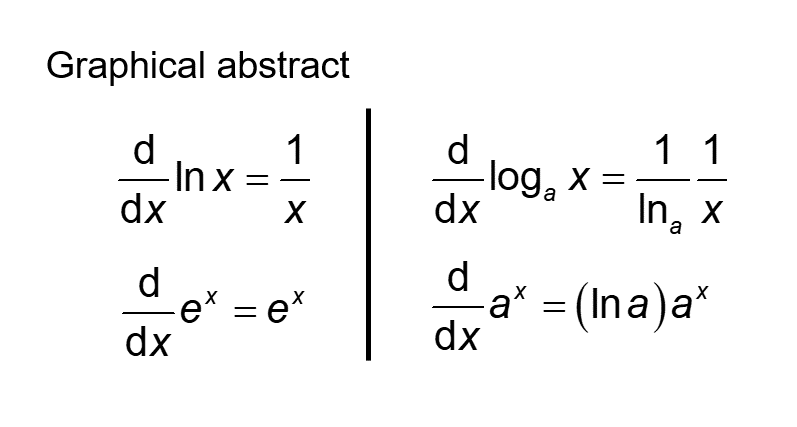
対数関数・指数関数の微分
対数関数と指数関数の微分について、以下の式が成立します。
本ページではこれらの導出過程を示します。
(注)lnは自然対数を意味します。
対数関数の微分
$$ \frac{\mathrm{d}}{\mathrm{d}x}\ln x=\frac{1}{x} \tag{1}$$
$$ \frac{\mathrm{d}}{\mathrm{d}x}\log_a x=\frac{1}{\ln a}\frac{1}{x} \tag{2}$$
指数関数の微分
$$ \frac{\mathrm{d}}{\mathrm{d}x}e^x=e^x \tag{3}$$
$$ \frac{\mathrm{d}}{\mathrm{d}x}a^x=\left( \ln a \right) a^x \tag{4}$$
自然対数の微分(Eq. (1)の導出)
Eq. (1)の導出には、自然対数の底(ネイピア数)\(e\)の定義を用います。
自然対数の底(ネイピア数)の定義
$$ \lim_{x \to \infty} \left( 1+\frac{1}{x} \right)^x =e \tag{1-1}$$
微分の定義(Eq. (1))に基づくと、対数関数(自然対数)\(\ln x\)の微分は以下の式で与えられます。
微分の定義
$$ \frac{\mathrm{d}f}{\mathrm{d}x} = \lim _{h \to 0} \frac{f(x+h)-f(x)}{h}
\tag{1-2} $$
$$ \frac{\mathrm{d}}{\mathrm{d}x} \ln x = \lim _{h \to 0} \frac{\ln (x+h) – \ln (x)}{h} $$
対数の性質(Eqs. (1-3~1-4))を用いて変形します。
対数の性質
$$ \ln \frac{a}{b} =\ln a -\ln b \tag{1-3} $$
$$ \ln a^b =b \ln a \tag{1-4} $$
$$
\begin{eqnarray}
\frac{\mathrm{d}}{\mathrm{d}x} \ln x
&=& \lim _{h \to 0} \frac{\ln (x+h) – \ln (x)}{h} \\
&=& \lim _{h \to 0} \frac{1}{h} \ln \frac{x+h}{x} \\
&=& \lim _{h \to 0} \ln \left( \frac{x+h}{x} \right) ^{\frac{1}{h}} \\
&=& \lim _{h \to 0} \ln \left( 1+\frac{h}{x} \right) ^{\frac{1}{h}} \\
\end{eqnarray}
$$
ここで、\(h \to +0\)と\(h \to -0\)の極限を分けて考えます。
まず、\(h \to +0\)の極限について考えます。
\(k\)を以下の式で定義すると、以下の式が成立します。
$$ k =\frac{x}{h} \tag{1-5} $$
対数関数の定義域より、\(x>0\)となるので、以下の式が成立します。
$$ (h \to +0) \to (k \to \infty)$$
$$
\begin{eqnarray}
\left( 1+\frac{h}{x} \right) ^{\frac{1}{h}}
&=& \left( 1+\frac{1}{k} \right) ^{\frac{1}{x}k} \\
&=& \left\{ \left( 1+\frac{1}{k} \right) ^k \right\}^{\frac{1}{x}}
\end{eqnarray}
$$
この関係式を代入し、Eqs. (1-1~1-4)を用いて変形します。
$$
\begin{eqnarray}
\frac{\mathrm{d}}{\mathrm{d}x} \ln x
&=& \lim _{h \to +0} \ln \left( 1+\frac{h}{x} \right) ^{\frac{1}{h}} \\
&=& \lim _{k \to \infty} \ln \left\{ \left( 1+\frac{1}{k} \right) ^k \right\}^{\frac{1}{x}} \\
&=& \lim _{k \to \infty} \frac{1}{x} \ln \left( 1+\frac{1}{k} \right) ^k \\
&=& \frac{1}{x} \ln e \\
&=& \frac{1}{x}
\end{eqnarray}
$$
続いて、\(h \to -0\)の極限について考えます。
\(l\)を以下の式で定義します。
$$ l =-\frac{x+h}{h} \tag{1-6} $$
対数関数の定義域より、\(x>0\)となるので、以下の式が成立します。
$$ (h \to +0) \to (l \to \infty) $$
Eq. (1-6)を\(h\)について解きます。
$$
\begin{eqnarray}
l &=& -\frac{x+h}{h} \\
-lh &=& x+h \\
-lh-h &=& x \\
-(l+1)h &=& x \\
h &=& -\frac{x}{l+1} \\
\end{eqnarray}
$$
この式を用いると、以下の式変形が成立します。
$$
\begin{eqnarray}
\left( 1+\frac{h}{x} \right) ^{\frac{1}{h}}
&=& \left( \frac{x+h}{x} \right) ^{-\frac{l+1}{x}} \\
&=& \left( \left( \frac{x+h}{x} \right)^{-1} \right)^{\frac{l+1}{x}} \\
&=& \left( \frac{x}{x+h} \right) ^{\left( l+1 \right) \frac{1}{x}} \\
&=& \left( \left( \frac{x+h-h}{x+h} \right) ^{l+1} \right) ^{\frac{1}{x}} \\
&=& \left( \left( \frac{x+h}{x+h}-\frac{h}{x+h} \right) ^{l+1} \right) ^{\frac{1}{x}} \\
&=& \left( \left( 1+\frac{1}{l} \right) ^{l+1} \right) ^{\frac{1}{x}} \\
\end{eqnarray}
$$
この関係式とを代入し、Eqs. (1-1~1-4)と指数の性質を用いて変形します。
指数の性質
$$ a^{b+c} =a^b a^c \tag{1-7} $$
$$
\begin{eqnarray}
\frac{\mathrm{d}}{\mathrm{d}x} \ln x
&=& \lim _{h \to -0} \ln \left( 1+\frac{h}{x} \right) ^{\frac{1}{h}} \\
&=& \lim _{l \to \infty} \ln \left( \left( 1+\frac{1}{l} \right) ^{l+1} \right) ^{\frac{1}{x}} \\
&=& \lim _{l \to \infty} \frac{1}{x} \ln \left( \left( 1+\frac{1}{l} \right) \left( 1+\frac{1}{l} \right) ^{l} \right) \\
&=& \frac{1}{x} \ln \left( 1e \right) \\
&=& \frac{1}{x} \ln e \\
&=& \frac{1}{x}
\end{eqnarray}
$$
\(h \to +0\)と\(h \to -0\)の極限を合わせると、Eq. (1)が導かれます。
$$
\frac{\mathrm{d}}{\mathrm{d}x}\ln x=\frac{1}{x} \tag{1}
$$
任意の底の対数関数の微分(Eq. (2)の導出)
任意の正の実数\(a\)を底とした対数関数の微分を考えます。
底の変換公式も用いて、自然対数の微分(Eq. (1))を用いるとEq. (2)が導かれます。
底の変換公式
$$ \log _a x =\frac{1}{\log _b a}\log _b x \tag{2-1} $$
$$
\begin{eqnarray}
\frac{\mathrm{d}}{\mathrm{d}x} \log _a x
&=& \frac{\mathrm{d}}{\mathrm{d}x} \frac{1}{\ln a}\ln x \\
&=& \frac{1}{\ln a} \frac{\mathrm{d}}{\mathrm{d}x} \ln x \\
&=& \frac{1}{\ln a} \frac{1}{x}\\
\end{eqnarray}
$$
$$
\frac{\mathrm{d}}{\mathrm{d}x}\log_a x=\frac{1}{\ln a}\frac{1}{x} \tag{2}
$$
指数関数の微分(Eq. (3)の導出)
Eq. (3)の導出には、対数微分法を用います。
Eq. (3-1)と対数の性質(Eq. (1-4))を用いると、Eq. (3)が導かれます。
対数微分法
$$ \frac{\mathrm{d}}{\mathrm{d}x} f(x) = f(x) \left\{ \frac{\mathrm{d}}{\mathrm{d}x} \ln \left( f(x) \right) \right\} \tag{3-1} $$

$$
\begin{eqnarray}
\frac{\mathrm{d}}{\mathrm{d}x} e^x
&=& e^x \left\{ \frac{\mathrm{d}}{\mathrm{d}x} \ln \left( e^x \right) \right\}\\
&=& e^x \left( \frac{\mathrm{d}}{\mathrm{d}x} x \ln e \right) \\
&=& e^x \\
\end{eqnarray}
$$
$$
\frac{\mathrm{d}}{\mathrm{d}x}e^x=e^x \tag{3}
$$
指数関数の微分(Eq. (4)の導出)
Eq. (4)の導出にも、対数微分法を用います。
対数微分法(Eq. (3-1))と対数の性質(Eq. (1-4))を用いると、Eq. (4)が導かれます。
$$
\begin{eqnarray}
\frac{\mathrm{d}}{\mathrm{d}x} a^x
&=& a^x \left\{ \frac{\mathrm{d}}{\mathrm{d}x} \ln \left( a^x \right) \right\}\\
&=& a^x \left( \frac{\mathrm{d}}{\mathrm{d}x} x \ln a \right) \\
&=& \left( \ln a \right) a^x \\
\end{eqnarray}
$$
$$
\frac{\mathrm{d}}{\mathrm{d}x}a^x=\left( \ln a \right) a^x \tag{4}
$$
関連ページ
高校生向け数学記事の一覧

