本記事では、最小二乗法による多変数線形回帰（線形重回帰）について解説します。
以下の記事では、\(n\)個のデータ点\(\left\{ \left( x_i , y_i \right) \right\}\)に関して、最小二乗法による線形単回帰分析について解説しました。
最小二乗法による線形単回帰分析では、以下の関係式が成立します。
$$ f(x)=ax+b \tag{1} $$
$$ a=\frac{\mathrm{Cov}[x,y]}{ \mathrm{Cov}[x,x]} \tag{2} $$
$$ b= E[y] – aE [x] \tag{3} $$
$$ E [x]=\frac{1}{n} \sum_i x_i \tag{4} $$
$$ \mathrm{Cov}[x,y]=E \left[ \left( x-E[x] \right) \left( y-E[y] \right) \right] \tag{5} $$
本記事では、\(y\)が1つの変数ではなく\(m\)個の変数(\(x_1,\cdots,x_m\)）に依存する場合を考え、最小二乗法による線形重回帰分析の関係式を導きます。
Webページでは要点となる式のみを表示いたしますので、詳細な導出過程については本ページ下部のpdfファイルを参照してください。
最小二乗法による線形重回帰
回帰式の関数形
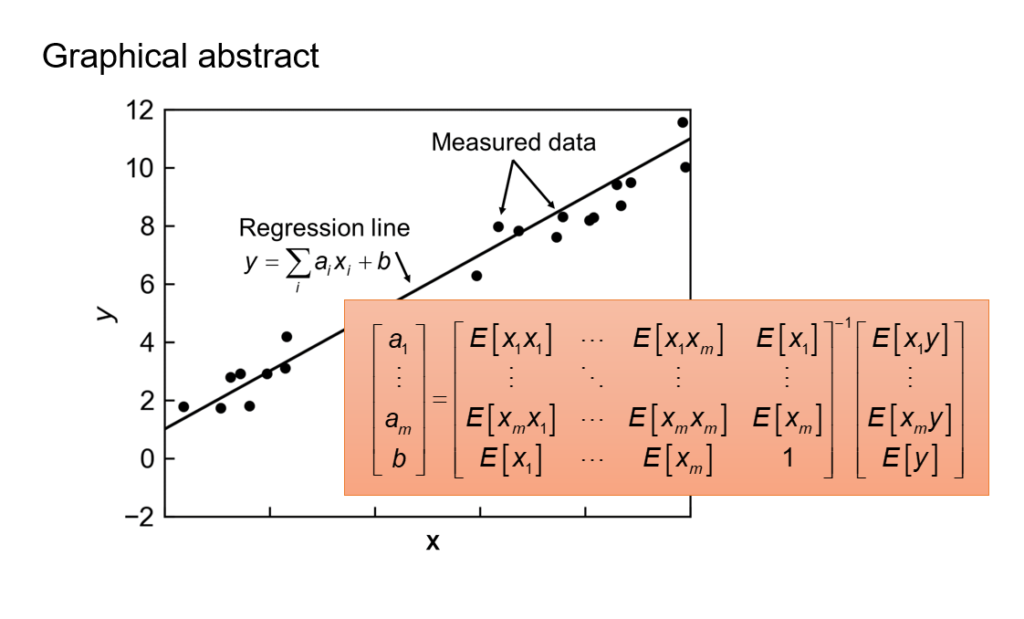
線形重回帰分析では、\(n\)個のデータ点\( \left\{ \left( x_{1 i},\cdots,x_{m,i}, y_i \right) \right\} \)を以下の式で回帰します。
$$ y=f(x_1, \cdots, x_m)=\sum_i a_i x_i+b \tag{1-1} $$
ベクトル表示すると、Eq. (1-1)は以下のように表現できます。
$$ y=f( \mathbf{x})= {}^\mathrm{t} \! \mathbf{a} \mathbf{x} +b \tag{1-2} $$
$$
\mathbf{x}_i=
{}^\mathrm{t} \!
\left[ \begin{array}{rr}
x_{1 i} & \cdots & x_{m i}
\end{array} \right] \tag{1-3}
$$
$$
\mathbf{a}=
{}^\mathrm{t} \! \left[
\begin{array}{rr}
a_1 & \cdots & a_m
\end{array} \right] \tag{1-4}
$$
左上付きのtは転置を意味しています。
二乗誤差
二乗誤差\(I\)は\(\mathbf{a}, b\)に依存する量であり、以下の式で表現されます。
$$ I(\mathbf{a}, b)=\sum_i \left( y_i- \left( {}^\mathrm{t} \! \mathbf{a} \mathbf{x} +b \right) \right) ^2 \tag{1-5} $$
回帰直線
\(I\)を最小化するために以下の方程式を考えます。
$$ \frac{\partial I}{\partial \mathbf{a}}=\mathbf{0} \tag{1-6} $$
$$ \frac{\partial I}{\partial b}=0 \tag{1-7} $$
この式を解くことで、\(\mathbf{a}, b\)を求めることができます。
詳細な計算過程については本ページ下部のpdfファイルを確認してください。
\(\mathbf{a}, b\)を与える関係式
Eqs. (1-6, 1-7)を計算すると以下の関係式が得られます。
この式の逆行列を求めることで、回帰式の係数を得ることができます。
$$
\left[
\begin{array}{c}
a_1 \\ \vdots \\ a_m \\b
\end{array}
\right]
=
\left[
\begin{array}{cccc}
E \left[ x_1 x_1 \right] & \cdots & E \left[ x_1 x_m \right] & E \left[ x_1 \right] \\
\vdots & \ddots & \vdots & \vdots \\
E \left[ x_m x_1 \right] & \cdots & E \left[ x_m x_m \right] & E \left[ x_m \right] \\
E \left[ x_1 \right] & \cdots & E \left[ x_m \right] & 1 \\
\end{array}
\right]
^{-1}
\left[
\begin{array}{c}
E \left[ x_1 y \right] \\ \vdots \\ E \left[ x_m y \right] \\ E \left[ y \right]
\end{array}
\right]
$$
ここで、\(E [x_i], \mathrm{Cov} [x,y]\)は\(\left\{ x_{ij} \right\}\)の平均と\(\left\{ \left( x_{ij} , y_j \right) \right\}\)の共分散であり、Eqs. (4, 5)で表現されます。
平均・分散・共分散について、より詳しく知りたい方は以下のページを参照してください。
