本記事では、結晶構造の対称性に由来した、直方晶、正方晶、立方晶、等方弾性体の弾性スティフネスの対称性について解説します。
弾性定はじめに
弾性スティフネス\(C_{ijkl}\)は4階のテンソルで、添え字の\(i, j, k\)は座標軸を表す1~3の値をとります。
\(C_{ijkl}\)は、結晶構造によらず下式の対称性を有し、独立な21個の成分を持ちます。
\[ C_{ijkl}=C_{jikl}=C_{ijlk}=C_{klij} \tag{1} \]

結晶材料では、それぞれの結晶構造の対称性に基づき、ここからさらに独立成分の数が減少します。
本稿では、直方晶、正方晶、立方晶、等方弾性体について、結晶構造の対称性と弾性スティフネスの対称性の関係を解説します。
六方晶の弾性スティフネスについては、こちらをご覧ください。
本稿では、特に断らない限り、Einstein(アインシュタイン)の総和規約を用いて式を表現します。
下式のように、同一項内に同じ記号の添え字が複数ある場合は、その記号について総和をとる点にご注意ください。
\[ a_i b_i c_j=\sum_i a_i b_i c_j \]
本稿では、\(C_{ijkl}\)を、Vogit表記を用いて、6×6の行列として表記します。

専門:材料力学、弾性論
数学:テンソル
直方晶
格子ベクトルと平行な3つの直交軸を\(x_i\) (\(i\)=1, 2, 3)と表現します。
弾性スティフネスの座標変換は下式で表現できます。
\[ C’_{ijkl}=C_{mnpq} l_{im} l_{jn} l_{kp} l_{lq} \tag{2} \]
\[ l_{ij}=\mathbf{e}’_i \cdot \mathbf{e}_j \]
ここで、\(C’_{ijkl}\)は変換後の座標における弾性定数、\(\mathbf{e}’_i\)は変換後の座標における\(x’_i\)軸の単位方向ベクトル、\(\mathbf{e}_i\)は変換前の座標における\(x_i\)軸の単位方向ベクトルです。
直方晶(Orthorhombic)は、任意の\(x_i\)軸の反転に対して不変のため、下図のような、\(x_i\)軸を反転し\(x’_i\)とする場合を考えます。
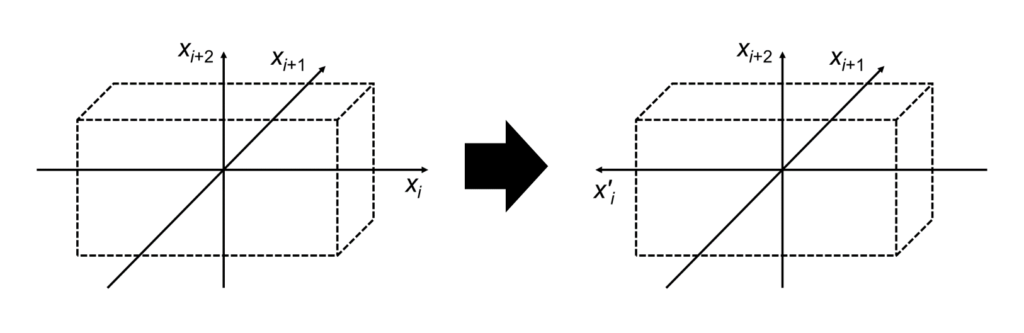
この座標変換における方向余弦\(l_{ij}\)は以下の式で与えられます。
\[
l_{ii}=-1 \\
l_{jk}=\delta_{jk} \ ((j, k) \neq (i, i))\\
\tag{3} \]
ここで、\(\delta_{ij}\)はKronecker(クロネッカー)のデルタであり、Eq. (3)にはEinsteinの総和規約を適用しません。
この座標変換により、\(C_{ijkl}\)は変化しないので、下式が成立します。
\[ C_{rskl}=C’_{rskl}=C_{mnpq} l_{rm} l_{sn} l_{kp} l_{lq} \tag{4} \]
\(l_{jj}\)は2つの添え字が同じ値でなれば0(Eq. (3))となるため、Eq. (4)は下式のように変形できます(Eq. (5)にはEinsteinの総和規約を適用しません)。
\[ C_{mnpq}=C_{mnpq} l_{mm} l_{nn} l_{pp} l_{qq} \tag{5} \]
\(l_{mm} l_{nn} l_{pp} l_{qq} \)は、Eq. (3)より、\(C_{mnpq}\)の添え字に含まれる\(i\)の数\(n_i\)によって下式の通り計算することができます。
\[ l_{mm} l_{nn} l_{pp} l_{qq} =
\begin{cases}
1 & (n_i \mathrm{\ is \ even}) \\
-1 & (n_i \mathrm{\ is \ odd}) \\
\end{cases} \tag{6} \]
この式を用いると、Eq. (5)から下式が得られます。
\[ C_{mnpq}=
\begin{cases}
C_{mnpq} & (n_i \mathrm{\ is \ even}) \\
-C_{mnpq} & (n_i \mathrm{\ is \ odd}) \\
\end{cases} \]
つまり、
\[ C_{mnpq}=
\begin{cases}
C_{mnpq} & (n_i \mathrm{\ is \ even}) \\
0 & (n_i \mathrm{\ is \ odd}) \\
\end{cases} \tag{7}\]
この式は任意の\(i\)について成立するため、\(C_{mnpq}\)は、添え字に含まれる何れかの数字の数(添え字内の登場回数)が奇数の場合、0となります。
つまり、\(j\), \(k\), \(l\)を互いに違う数字とした場合、下式が成立します。
\[ C_{jjjk}=C_{jjkl}=C_{jkjl}=0 \tag{8}\]
当然、Eq. (1)に基づき、Eq. (8)の添え字を並び変えた項も0となります。
これらの結果を整理すると、\(C_{ijkl}\)の独立成分数は9個となり、下式で表現できます。
\[
\begin{eqnarray}
\mathbf{C}
&=&
\left[
\begin{array}{cccccc}
C_{1111} & C_{1122} & C_{3311} & & & \\
C_{1122} & C_{2222} & C_{2233} & & \mathrm{O} & \\
C_{3311} & C_{2233} & C_{3333} & & & \\
& & & C_{2323} & 0 & 0 \\
& \mathrm{O} & & 0 & C_{3131} & 0 \\
& & & 0 & 0 & C_{1212} \\
\end{array}
\right] \\
&=&
\left[
\begin{array}{cccccc}
C_{11} & C_{12} & C_{31} & & & \\
C_{12} & C_{22} & C_{23} & & \mathrm{O} & \\
C_{31} & C_{23} & C_{33} & & & \\
& & & C_{44} & 0 & 0 \\
& \mathrm{O} & & 0 & C_{55} & 0 \\
& & & 0 & 0 & C_{66} \\
\end{array}
\right]
\end{eqnarray}
\tag{9} \]
\(\mathbf{C}\)は\(C_{ijkl}\)の行列表記を表しています。
正方晶
正方晶(Tetragonal)では、直方晶の対称性に加えて、\(x_1\)軸と\(x_2\)軸の交換に対して不変となります。
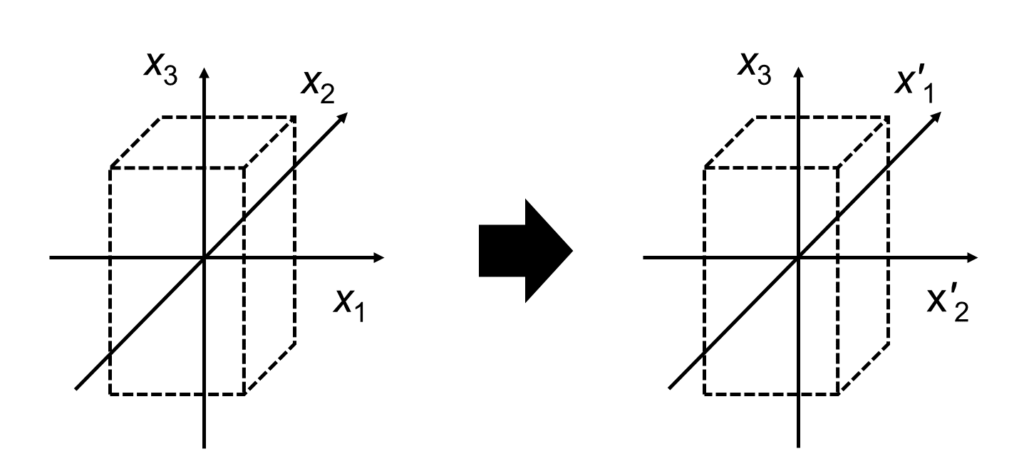
上図のような座標変換を考えると方向余弦\(l_{ij}\)は以下の式で与えられます。
\[
l_{12}=l_{21}=l_{33}=1 \\
\mathrm{Others}=0\\
\tag{10} \]
Eq. (2)に代入して整理すると、以下の関係式が得られます。
\[
C_{1111}=C_{2222} \\
C_{2233}=C_{3311} \\
C_{2323}=C_{3131} \\
\tag{11} \]
これにより、\(C_{ijkl}\)の独立成分数は6個となり、下式のように表現できます。
\[
\mathbf{C}
=
\left[
\begin{array}{cccccc}
C_{11} & C_{12} & C_{23} & & & \\
C_{12} & C_{11} & C_{23} & & \mathrm{O} & \\
C_{23} & C_{23} & C_{33} & & & \\
& & & C_{44} & 0 & 0 \\
& \mathrm{O} & & 0 & C_{44} & 0 \\
& & & 0 & 0 & C_{66} \\
\end{array}
\right]
\tag{12} \]
立方晶
立方晶(Cubic)では、正方晶の対称性に加えて、\(x_1\)軸と\(x_3\)軸の交換に対して不変となります。
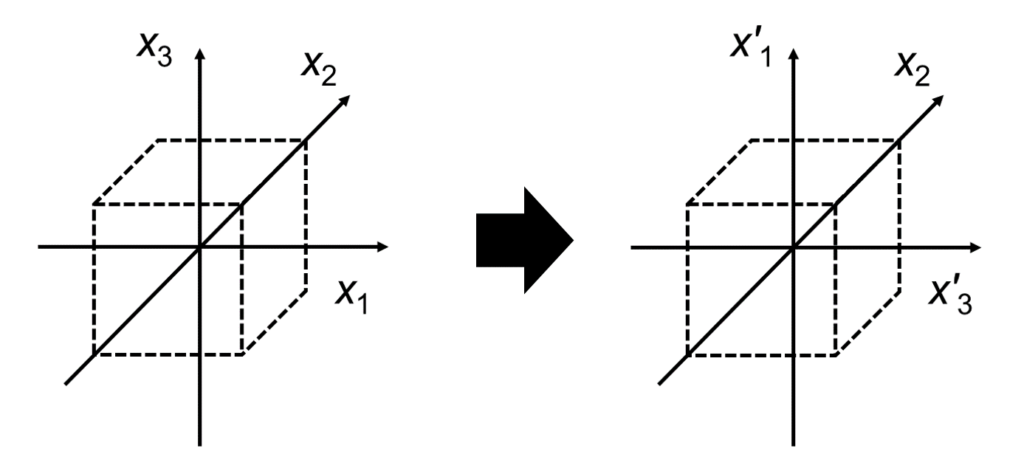
上図のような座標変換を考えると、方向余弦\(l_{ij}\)は以下の式で与えられます。
\[
l_{13}=l_{31}=l_{22}=1 \\
\mathrm{Others}=0\\
\tag{13} \]
Eq. (2)に代入して整理すると、以下の関係式が得られます。
\[
C_{1111}=C_{3333} \\
C_{1122}=C_{2233} \\
C_{1212}=C_{2323} \\
\tag{14} \]
これにより、\(C_{ijkl}\)の独立成分数は3個となり、下式のように表現できます。
\[
\mathbf{C}=
\left[
\begin{array}{cccccc}
C_{11} & C_{12} & C_{12} & & & \\
C_{12} & C_{11} & C_{12} & & \mathrm{O} & \\
C_{12} & C_{12} & C_{11} & & & \\
& & & C_{44} & 0 & 0 \\
& \mathrm{O} & & 0 & C_{44} & 0 \\
& & & 0 & 0 & C_{44} \\
\end{array}
\right]
\tag{15} \]
等方弾性体
等方弾性体は、立方晶の対称性に加えて、任意の回転に対する不変性を有します。
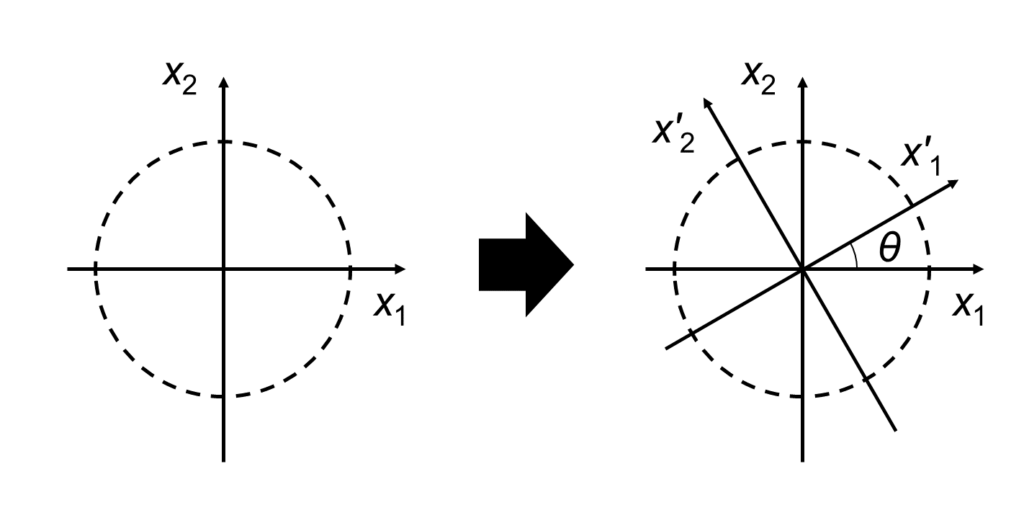
上図の座標回転を考えた場合、\(l_{ij}\)は以下の式で与えられます。
\[ l_{11}=\cos \theta \\
l_{12}=\sin \theta \\
l_{21}=-\sin \theta \\
l_{22}=\cos \theta \\
l_{33}=1 \\
\mathrm{Others}=0\\
\tag{16} \]
Eq. (2)に代入して整理すると、以下の関係式が得られます。
\[ C_{1111}=C_{1122}+2C_{1212} \tag{17} \]
これにより、\(C_{ijkl}\)の独立成分数は2個となり、下式のように表現できます。
\[
\mathbf{C}=
\left[
\begin{array}{cccccc}
\lambda + 2 \mu & \lambda & \lambda & & & \\
\lambda & \lambda + 2 \mu & \lambda & & \mathrm{O} & \\
\lambda & \lambda & \lambda + 2 \mu & & & \\
& & & \mu & 0 & 0 \\
& \mathrm{O} & & 0 & \mu & 0 \\
& & & 0 & 0 & \mu \\
\end{array}
\right]
\tag{18} \]
ここで、\(\lambda, \mu \)はラメ定数と呼ばれ、等方弾性体の弾性特性の記述によく用いられる記号です。
まとめ
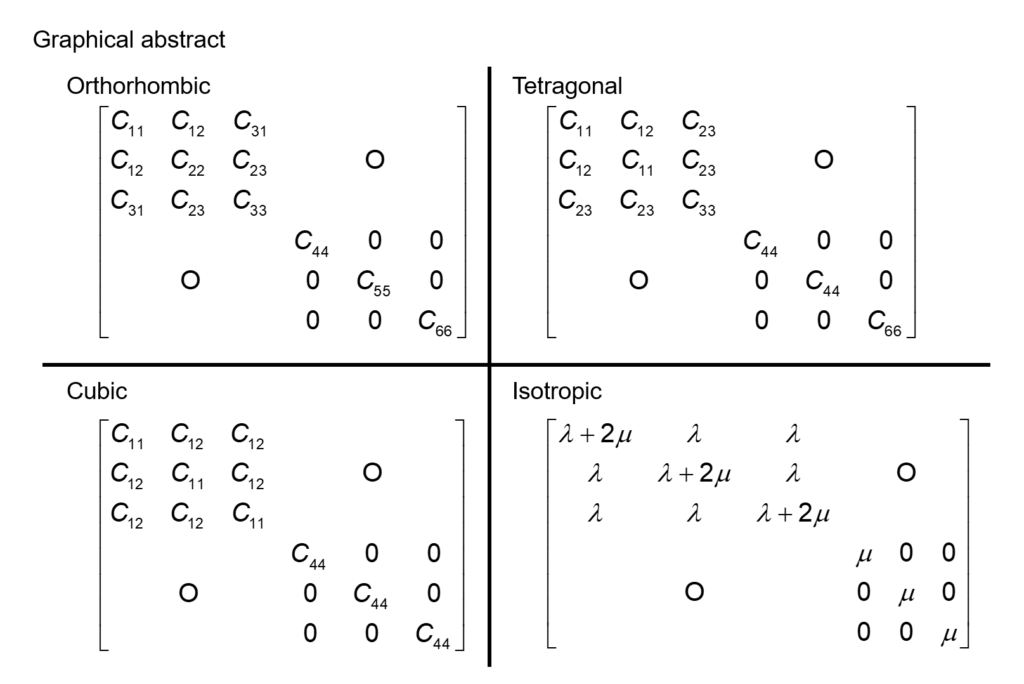
直方晶、正方晶、立方晶、等方弾性体の弾性特性スティフネスは、それぞれの結晶構造の対称性により、下式のように表現することができます。
- 直方晶
-
\[
\mathbf{C}=
\left[
\begin{array}{cccccc}
C_{11} & C_{12} & C_{31} & & & \\
C_{12} & C_{22} & C_{23} & & \mathrm{O} & \\
C_{31} & C_{23} & C_{33} & & & \\
& & & C_{44} & 0 & 0 \\
& \mathrm{O} & & 0 & C_{55} & 0 \\
& & & 0 & 0 & C_{66} \\
\end{array}
\right]
\tag{9} \] - 正方晶
-
\[
\mathbf{C}
=
\left[
\begin{array}{cccccc}
C_{11} & C_{12} & C_{23} & & & \\
C_{12} & C_{11} & C_{23} & & \mathrm{O} & \\
C_{23} & C_{23} & C_{33} & & & \\
& & & C_{44} & 0 & 0 \\
& \mathrm{O} & & 0 & C_{44} & 0 \\
& & & 0 & 0 & C_{66} \\
\end{array}
\right]
\tag{12} \] - 立方晶
-
\[
\mathbf{C}=
\left[
\begin{array}{cccccc}
C_{11} & C_{12} & C_{12} & & & \\
C_{12} & C_{11} & C_{12} & & \mathrm{O} & \\
C_{12} & C_{12} & C_{11} & & & \\
& & & C_{44} & 0 & 0 \\
& \mathrm{O} & & 0 & C_{44} & 0 \\
& & & 0 & 0 & C_{44} \\
\end{array}
\right]
\tag{15} \] - 等方弾性体
-
\[
\mathbf{C}=
\left[
\begin{array}{cccccc}
\lambda + 2 \mu & \lambda & \lambda & & & \\
\lambda & \lambda + 2 \mu & \lambda & & \mathrm{O} & \\
\lambda & \lambda & \lambda + 2 \mu & & & \\
& & & \mu & 0 & 0 \\
& \mathrm{O} & & 0 & \mu & 0 \\
& & & 0 & 0 & \mu \\
\end{array}
\right]
\tag{18} \]
詳細な式展開(PDFファイル)
以下のpdfファイルより、本記事に関係する式展開の詳細をご確認頂けます。
適宜ご参照ください。
