金属材料に対して一軸引張試験を行うと、弾性限に到達後、塑性変形が進行し、最終的に破断に至ります。塑性変形の初期では試験片のいたるところで変形が進行し、マクロ的には平行部の全体において均一な変形が生じると見做すことができます。変形が進行すると、平行部の一部においてくびれが形成し、変形がくびれ領域に局在化します。ここでは、一軸引張試験におけるくびれの発生条件についてまとめます。各関係式の導出過程は以下のPDFファイルをご確認ください。
本ページでまとめています、くびれの発生条件に付きまして、局所変形の進行条件という観点からの導出を以下のページで紹介しております。併せてご確認ください。
状況設定・記号の定義
状況設定
下図のように一軸引張試験においてくびれが発生するときを考える。
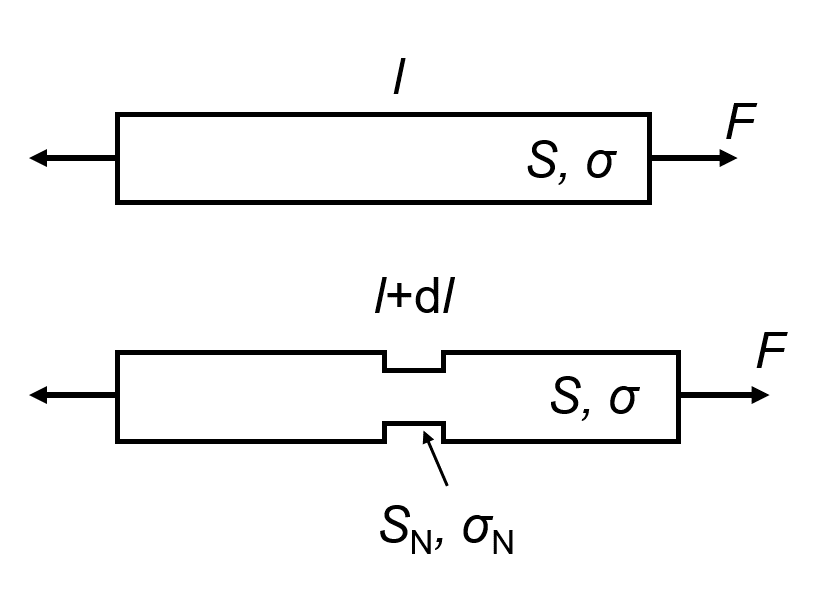
記号の定義
\(F\): 外力(Force)
\(l\): 平行部の長さ
\(S\): 平行部の断面積
\(S_{\mathrm{N}}\): くびれ部の断面積
\(\sigma_{\mathrm{n}}\): 公称応力(Nominal stress)
\(\sigma_{\mathrm{t}}\): 真応力(True stress)
\(\sigma_{\mathrm{N}}\): くびれ部に作用する真応力
\(\epsilon_{\mathrm{n}}\): 公称ひずみ(Nominal strain)
\(\epsilon_{\mathrm{t}}\): 真ひずみ(True strain)
くびれの発生条件
くびれの発生条件は、以下のようになります。導出過程については、本ページ上部のpdfファイルをご確認ください。
“外力-長さ”での表現
$$ \frac{\mathrm{d}F}{\mathrm{d}l}=0 \tag{1} $$
“公称応力-公称ひずみ”での表現
$$ \frac{\mathrm{d}\sigma_{\mathrm{n}}}{\mathrm{d}\epsilon_{\mathrm{n}}}=0 \tag{2} $$
“真応力-真ひずみ”での表現
$$ \frac{\mathrm{d}\sigma_{\mathrm{t}}}{\mathrm{d}\epsilon_{\mathrm{t}}}= \sigma_{\mathrm{t}} \tag{3} $$
\(n\)乗硬化則が成立する場合
\(n\)乗硬化則:
$$ \sigma_{\mathrm{t}} =C\epsilon_{\mathrm{t}}^n \tag{4} $$
が成立する場合、Eq. (3)からくびれの発生条件は以下の式で表現することができます。
$$ n= \epsilon_{\mathrm{t}} \tag{5} $$
なお、ここで、\(C\)は\(n\)乗硬化則の係数です。

