本記事では、X線結晶構造解析の基礎理論を示します。
Webページ上では要点のみを示しますので、細かな式展開については本ページ下部のpdfファイルをご確認ください。
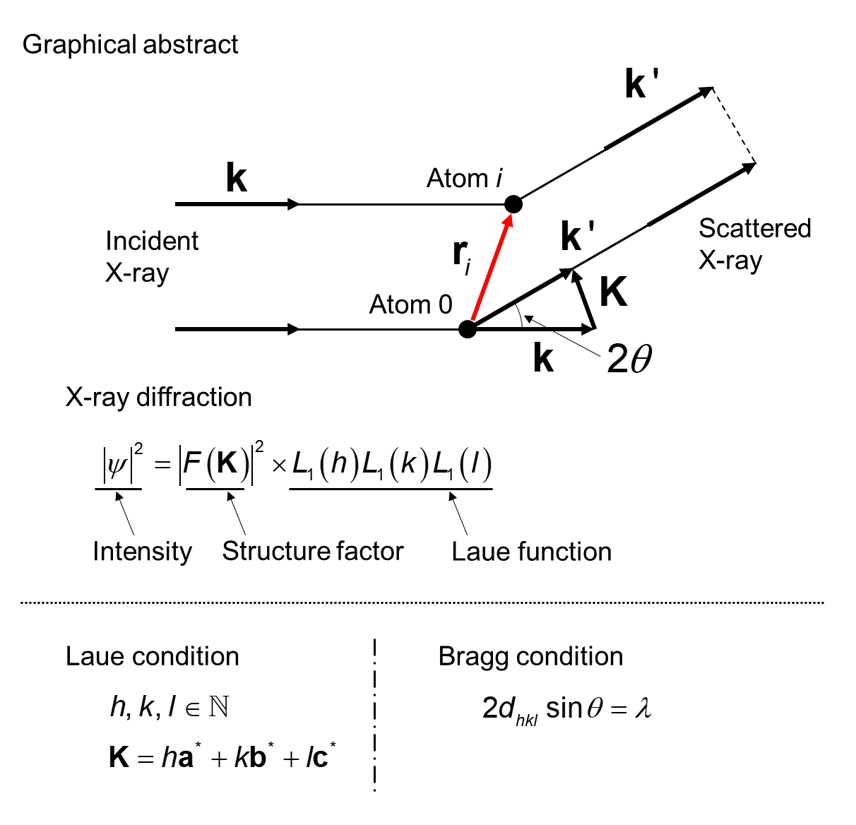
X線の回折
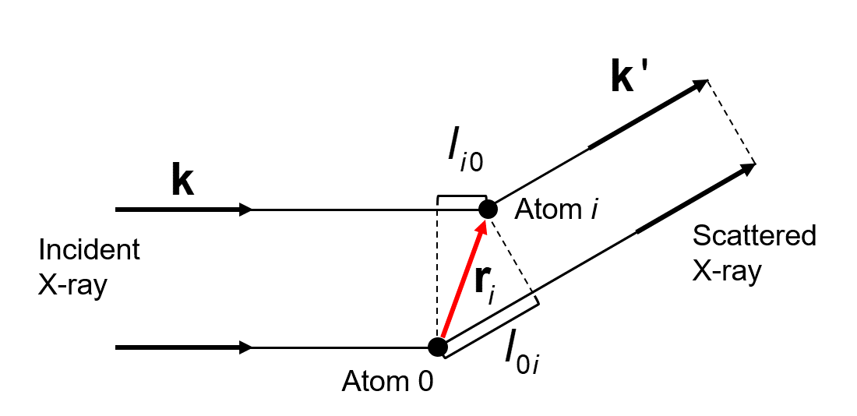
上図のように、原子0と原子\(i\)で散乱されたX線の検出位置における変位を\(\psi_0, \psi_i\)、入射X線と散乱X線の波長ベクトルを\(\mathbf{k}, \mathbf{k’}\)、原子\(i\)で散乱されたX線の振幅を\(A_i\)、X線の波長を\(\lambda\)、原子0を基準とした原子\(i\)の位置ベクトルを\(\mathbf{r}_i\)とすると、以下の関係式が成立します。
$$ \psi_i=\frac{A_i}{A_0} \psi_0 \exp \left( i \mathbf{K} \cdot \mathbf{r}_i \right) \tag{1-1}$$
$$ \mathbf{K} =\mathbf{k’} – \mathbf{k} \tag{1-2}$$
$$ \left| \mathbf{k} \right|=\left| \mathbf{k’} \right|=\frac{2\pi}{\lambda} \tag{1-3}$$
X線の照射範囲の全原子について\(\psi_i\)の総和をとると以下の式が成立します。
\(\psi_i\)の総和
$$ \psi=\sum_i \psi_i =\frac{\psi_0}{A_0} \sum_i A_i \exp \left( -i \mathbf{K} \cdot \mathbf{r}_i \right) \tag{1-4} $$
Eq. (1-4)の後半は\(A_i\)のフーリエ変換に相当します。
結晶からの回折
下図のように\(N_{\mathrm{a}} \times N_{\mathrm{b}} \times N_{\mathrm{c}} \)個の単位胞で形成される領域からの回折を考え、Eq. (1-4)の総和を単位胞の和と単位胞内の元素の和に分割します。
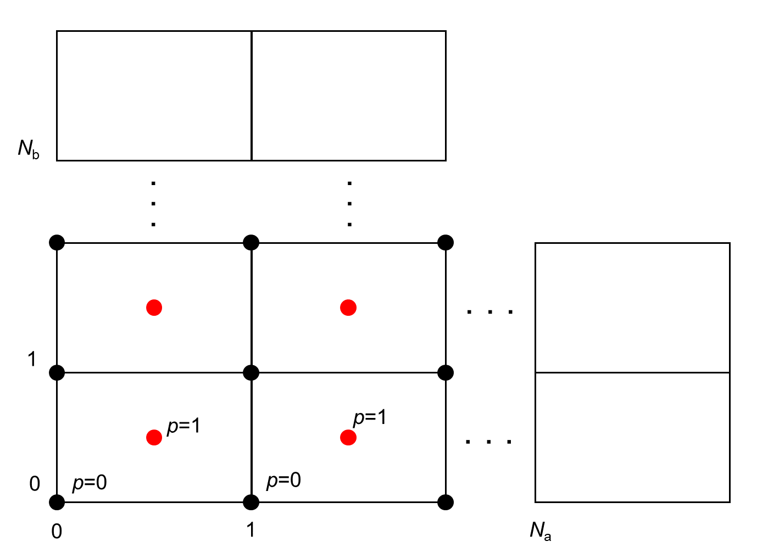
以下のように規則構造あるいはランダム固溶体を考えると、Eq. (1-4)は以下のように変形できます。
【規則構造】
\(A_i\)は元素種に依存するため、\(A_i\)は\(p\)のみに依存します。
【ランダム固溶体】
\(A_i\)を厳密に取り扱うことは困難であるため、平均場を考え\(A_i\)が\(i\)に依存しないものとします。
$$ \psi=\frac{\psi_0}{A_0} F \left( \mathbf{K} \right) \left\{ \sum_{u=0}^{N_{\mathrm{a}}-1} \sum_{v=0}^{N_{\mathrm{b}}-1} \sum_{w=0}^{N_{\mathrm{c}}-1} \exp \left( -i \mathbf{K} \cdot \mathbf{r}_{uvw}^{\mathrm{u}} \right)\right\} \tag{2-1}$$
$$ \mathbf{r}_{uvw}^{\mathrm{u}}=u\mathbf{a}+v\mathbf{b}+w\mathbf{c} \tag{2-2}$$
$$ \mathbf{K}=h\mathbf{a}^{*}+k\mathbf{b}^{*}+l\mathbf{c}^{*} \tag{2-3}$$
結晶構造因子(Structure factor)\(F \left( \mathbf{K} \right)\)
$$ F \left( \mathbf{K} \right)=\sum_p A_p \exp \left( -i \mathbf{K} \cdot \mathbf{r}_{p}^{\mathrm{a}} \right) \tag{2-4}$$
ここで、\(\mathbf{a}, \mathbf{b}, \mathbf{c}\)は単位胞の基本並進ベクトル、\(\mathbf{a}^{*}, \mathbf{b}^{*}, \mathbf{c}^{*}\)は逆格子ベクトル、\(h, k, l\)は任意の実数です。
Eq. (2-1)の\(u, v, w\)に関する和は等比級数であるため、回折X線の強度\(\left| \psi \right|^2 \)は以下の式で与えられます。
\(u, v, w\)に関する和(等比級数)
$$ \sum_{u=0}^{N_{\mathrm{a}}-1} \sum_{v=0}^{N_{\mathrm{b}}-1} \sum_{w=0}^{N_{\mathrm{c}}-1} \exp \left( -i \mathbf{K} \cdot \mathbf{r}_{uvw}^{\mathrm{u}} \right)= \exp \left( -i \pi \left\{ h \left( N_{\mathrm{a}} -1 \right) + k \left( N_{\mathrm{b}} -1 \right) +l \left( N_{\mathrm{c}} -1 \right) \right\}\right) \frac{\sin \pi h N_{\mathrm{a}}}{\sin \pi h} \frac{\sin \pi k N_{\mathrm{b}}}{\sin \pi k} \frac{\sin \pi l N_{\mathrm{c}}}{\sin \pi l} \tag{2-5} $$
強度\(\left| \psi \right| ^2\)
$$ \left| \psi \right| ^2 =\left| F \left( \mathbf{K} \right) \right| ^2 L_1\left( h \right) L_1\left( k \right) L_1\left( l \right) \tag{2-6}$$
Laue関数(ラウエ関数:Laue function、Laueの回折関数)\(L_1\left( h \right) L_1\left( k \right) L_1\left( l \right) \)
$$ L_1\left( h \right) =\frac{\sin^2 \pi h N_{\mathrm{a}}}{\sin^2 \pi h}, L_1\left( k \right) =\frac{\sin^2 \pi k N_{\mathrm{b}}}{\sin^2 \pi k}, L_1\left( l \right) =\frac{\sin^2 \pi l N_{\mathrm{c}}}{\sin^2 \pi l} \tag{2-7}$$
Laue条件
Eq. (2-7)の\( L_1\left( h \right) \)は以下の性質を有しており、概形は下図のようになります。
\( L_1\left( h \right) \)の性質
$$ L_1\left( n+h \right) = L_1\left( h \right) \tag{3-1}$$
$$ L_1\left( n \right) = N_{\mathrm{a}}^2 \tag{3-2}$$
$$ L_1\left( n \pm \frac{1}{N_{\mathrm{a}}} \right) = 0 \tag{3-3}$$
ここで、\(n\)は整数です。
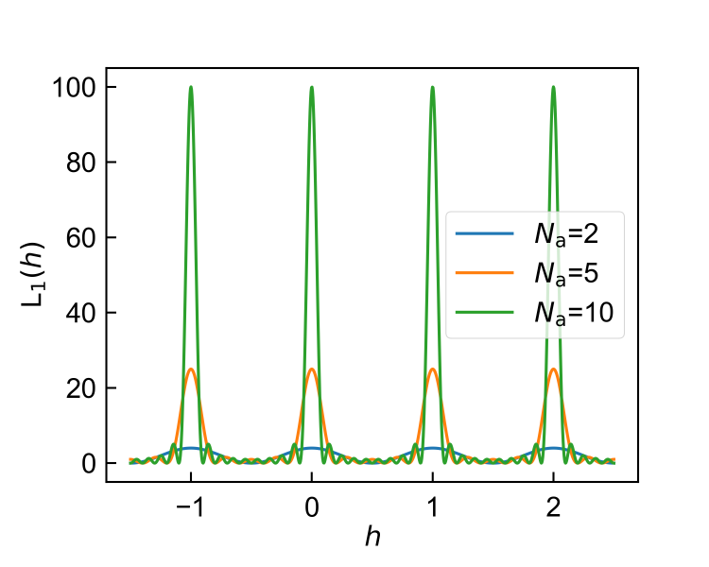
このように、\( L_1\left( h \right) \)は\( h \)が整数となるところで、高さ\( N_{\mathrm{a}}^2 \)、幅\( 2/N_{\mathrm{a}} \)のピークを持ちます。
\( N_{\mathrm{a}} \)が十分に大きい場合、\( h \)が整数となるピーク以外は無視することができます。
\( k, l \)についても同様の議論が成立するため、\(\left| \psi \right| ^2\)が有効な値を持つのは、\( h, k, l \)がすべて整数となる場合です。
この条件はLaue条件(ラウエ条件:Laue condition)と呼ばれ、\(\mathbf{K}\)が逆格子点にちょうど乗る事を意味します。
Laue条件
$$ h, k, l \in \mathbb{N} \tag{3-4} $$
$$ \mathbf{K}=h\mathbf{a}^{*}+k\mathbf{b}^{*}+l\mathbf{c}^{*} \tag{2-3} $$
ここで、\(\mathbb{N}\)は自然数全体の集合です。
Bragg条件と結晶構造解析
\(\mathbf{k}\)と\(\mathbf{k’}\)のなす角を\(2\theta\)とすると、Eqs. (1-2, 1-3)より以下の式が成立します。
$$ \lambda = 2 \frac{2 \pi}{\left| \mathrm{K} \right|} \sin \theta \tag{4-1} $$
Laue条件より、\( h, k, l \)が整数化され、\(\mathbf{K}\)が逆格子点上のベクトルとなるため、(h k l)の面間隔\(d_{hkl}\)は以下の式で与えられます。
面間隔\(d_{hkl}\)
$$ d_{hkl}= \frac{2 \pi}{\left| \mathrm{K} \right|} \tag{4-2} $$
Eq. (4-2)をEq. (4-1)に代入すると、以下の式が成立します。
Bragg条件(ブラッグ条件:Bragg condition)
$$ \lambda = 2 d_{hkl} \sin \theta \tag{4-3} $$
Eq. (4-3)はLaue条件の別表現であり、Bragg条件と呼ばれています。
Eq. (4-3)を変形すると、以下の関係式が得られます。
$$ 2\theta = 2\arcsin \left( \frac{\lambda}{2 d_{hkl}} \right) \tag{4-4} $$
Eq. (4-4)より、\(2\theta\)と\(d_{hkl}\)が一意に対応します。
よって、X線源と検出器の角度を変えながら回折X線の強度を測定し、ピーク角度を解析することによって、結晶構造と格子定数を解析することができます。
なお、\(\left| \psi \right| ^2\)はLaue関数だけでなく結晶構造因子(\(F \left( \mathbf{K} \right) \))の影響も受ける(Eq. (2-6))ため、Laue条件(Bragg条件)を満たす場合でも、\(F \left( \mathbf{K} \right) =0\)となる場合(消滅則)、ピークは検出されません。
