本記事では、正規分布の確率密度関数を、ガウス関数の一般形から導きます。
Webページでは要点となる式のみを表示いたしますので、詳細な導出過程については本ページ下部のpdfファイルを参照してください。
正規分布(ガウス分布)と正規分布
多くの現象は正規分布(ガウス分布: Gausian distribution)に従うことが知られています。
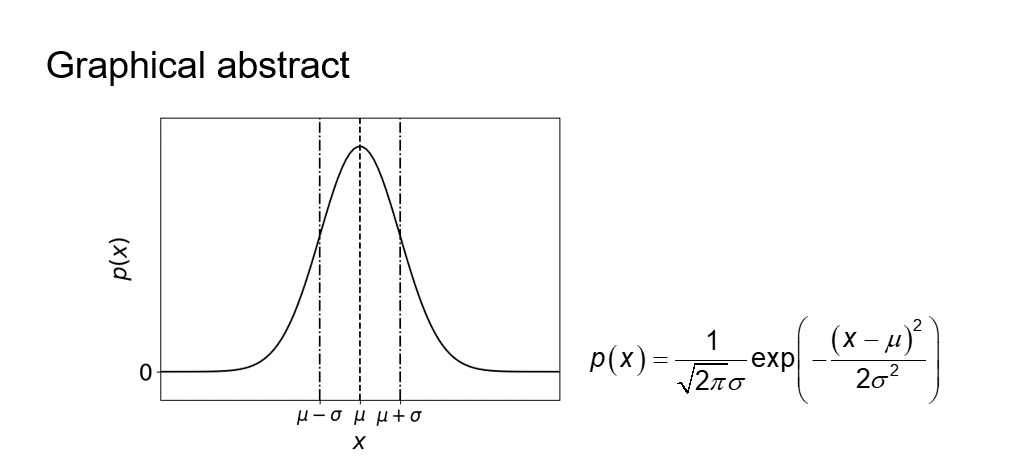
正規分布に従うデータ\(x\)に関する確率密度関数\(p(x)\)の概形は下図のようになります。
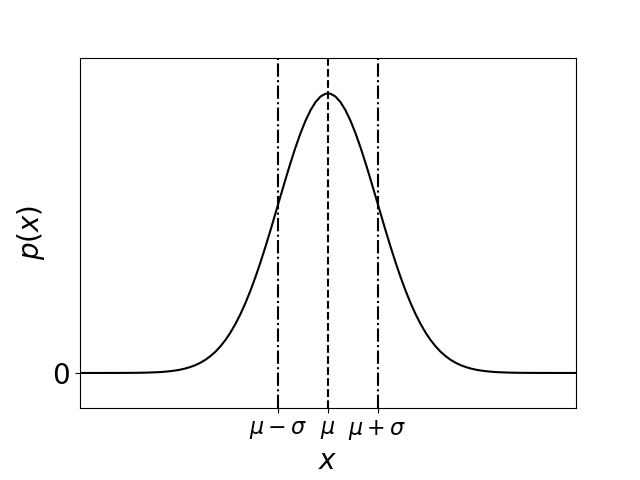
また、\(p(x)\)は以下の式で表現されます。
$$ p(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp \left( -\frac{\left( x-\mu \right)^2}{2\sigma^2}\right) \tag{1} $$
ここで、\(\mu\)は\(x\)の平均、\(\sigma\)は\(x\)の標準偏差です。
Eq. (1)はガウス関数の一種であり、一般的なガウス関数は以下の式で与えられます。
$$ f(x)=a \exp \left( -\frac{\left( x-b \right)^2}{c^2}\right) \tag{2} $$
このページではEq. (2)からEq. (1)を導きます。
導出
詳細な計算過程については本ページ下部のpdfファイルを確認してください。
ガウス積分
ガウス積分として以下の式が成立することが知られています。
$$ \int_{-\infty}^{\infty} \exp\left( -x^2 \right) \mathrm{d}x=\sqrt{\pi} \tag{1-1} $$
この式の導出では左辺の二乗を考えます。
$$ \left( \int_{-\infty}^{\infty} \exp\left( -x^2 \right) \mathrm{d}x \right) ^2=\left( \int_{-\infty}^{\infty} \exp\left( -x^2 \right) \mathrm{d}x \right) \left( \int_{-\infty}^{\infty} \exp\left( -x^2 \right) \mathrm{d}x \right) $$
積分内では積分変数を書き換えても問題ないので、以下のように変形できます。
$$
\begin{eqnarray}
&& \left( \int_{-\infty}^{\infty} \exp\left( -x^2 \right) \mathrm{d}x \right) ^2 \\
&=& \left( \int_{-\infty}^{\infty} \exp\left( -x^2 \right) \mathrm{d}x \right) \left( \int_{-\infty}^{\infty} \exp\left( -y^2 \right) \mathrm{d}y \right) \\
&=& \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \exp \left( -\left( x^2 + y^2 \right) \right) \mathrm{d}x \mathrm{d}y \\
\end{eqnarray}
$$
極座標変換します。
$$
\begin{eqnarray}
\left( \int_{-\infty}^{\infty} \exp\left( -x^2 \right) \mathrm{d}x \right) ^2
&=& \int_{0}^{2\pi}\mathrm{d}\theta \int_{0}^{\infty} r\exp \left( -r^2 \right) \mathrm{d}r \\
&=& 2\pi \int_{0}^{\infty} r\exp \left( -r^2 \right) \mathrm{d}r \\
\end{eqnarray}
$$
以下の微分を考えると、以下の積分が成立します。
$$ \frac{\mathrm{d}}{\mathrm{d}x} \left\{ -\frac{1}{2}\exp \left( -x^2 \right) \right\}=x \exp \left( -x^2 \right) $$
$$ \int_{0}^{\infty} r\exp \left( -r^2 \right) \mathrm{d}r =\frac{1}{2} \tag{1-2} $$
この積分を用いる事で以下の式が得られます。
$$ \left( \int_{-\infty}^{\infty} \exp\left( -x^2 \right) \mathrm{d}x \right) ^2=\pi $$
Eq. (1-1)の被積分関数はすべての定義域で正なので、ガウス関数が導かれます。
$$ \int_{-\infty}^{\infty} \exp\left( -x^2 \right) \mathrm{d}x=\sqrt{\pi} \tag{1-1} $$
規格化
Eq. (1-1)は確率密度関数なので、全区間積分を考えると以下の式が成立します。
$$ \int_{-\infty}^{\infty} a \exp \left( -\frac{\left( x-b \right)^2}{c^2}\right) \mathrm{d}x=1 \tag{2-1} $$
この式を解くと、以下の式が得られます。
$$ a=\frac{1}{\sqrt{\pi}c} \tag{2-2} $$
平均値
\(x\)の平均値\(\mu\)は以下の式で与えられます。
$$ \mu=\int_{-\infty}^{\infty} x a \exp \left( -\frac{\left( x-b \right)^2}{c^2}\right) \mathrm{d}x \tag{3-1} $$
この式から、以下の関係式が導かれます。
$$ b=\mu \tag{3-2} $$
分散
\(x\)の分散\(\sigma^2\)は以下の式で与えられます。
$$ \sigma ^2=\int_{-\infty}^{\infty} \left( x-\mu \right) ^2 a \exp \left( -\frac{\left( x-b \right)^2}{c^2}\right) \mathrm{d}x \tag{4-1} $$
この式から、以下の関係式が導かれます。
$$ c=\sqrt{2}\sigma \tag{4-2} $$
正規分布
Eq. (2)にEqs. (2-2, 3-2, 4-2)を代入すると、Eq. (1)が得られます。
$$ p(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp \left( -\frac{\left( x-\mu \right)^2}{2\sigma^2}\right) \tag{1} $$
