本記事では、部分積分について導出過程を示します。
対象読者:高校生
必要な知識:高校数学 微分、積分
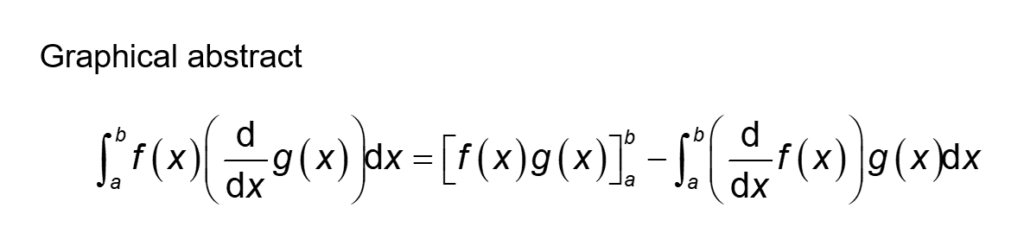
部分積分
部分積分の関係式として、以下の式が成立します。
$$ \int_a^b f \frac{\mathrm{d}g}{\mathrm{d}x} \mathrm{d}x= \left[ f(x)g(x) \right] _a ^b -\int_a^b \frac{\mathrm{d}f}{\mathrm{d}x} g \mathrm{d}x \tag{1}$$
Eq. (1)の導出
Eq. (1)の導出にあたり、関数積の微分の積分を考えます。
関数積の微分
$$
\frac{\mathrm{d}}{\mathrm{d}x} f(x)g(x) = \frac{\mathrm{d}f}{\mathrm{d}x} g+ f \frac{\mathrm{d}g}{\mathrm{d}x}
\tag{1-1}
$$

$$
\begin{eqnarray}
\int _a^b \frac{\mathrm{d}}{\mathrm{d}x} fg \mathrm{d}x
&=& \int _a^b \frac{\mathrm{d}f}{\mathrm{d}x} g+ f \frac{\mathrm{d}g}{\mathrm{d}x} \mathrm{d}x \\
&=& \int _a^b \frac{\mathrm{d}f}{\mathrm{d}x} g \mathrm{d}x+ \int _a^b f \frac{\mathrm{d}g}{\mathrm{d}x} \mathrm{d}x \\
\end{eqnarray}
$$
積分の定義より、以下の式が成立します。
積分の定義
$$
\int _a^b \frac{\mathrm{d}f}{\mathrm{d}x} \mathrm{d}x = \left[ f(x) \right] _a^b \tag{1-2}
$$
$$ \int _a^b \frac{\mathrm{d}}{\mathrm{d}x} fg \mathrm{d}x = \left[ f(x)g(x) \right] _a^b $$
この式を用いて、式を整理するとEq. (1)が導かれます。
$$
\begin{eqnarray}
\int _a^b \frac{\mathrm{d}}{\mathrm{d}x} fg \mathrm{d}x &=& \int _a^b \frac{\mathrm{d}f}{\mathrm{d}x} g \mathrm{d}x+ \int _a^b f \frac{\mathrm{d}g}{\mathrm{d}x} \mathrm{d}x \\
\left[ f(x)g(x) \right] _a^b &=& \int _a^b \frac{\mathrm{d}f}{\mathrm{d}x} g \mathrm{d}x+ \int _a^b f \frac{\mathrm{d}g}{\mathrm{d}x} \mathrm{d}x \\
\int _a^b f \frac{\mathrm{d}g}{\mathrm{d}x} \mathrm{d}x &=& \left[ f(x)g(x) \right] _a^b – \int _a^b \frac{\mathrm{d}f}{\mathrm{d}x} g \mathrm{d}x \\
\end{eqnarray}
$$
$$ \int_a^b f \frac{\mathrm{d}g}{\mathrm{d}x} \mathrm{d}x= \left[ f(x)g(x) \right] _a ^b -\int_a^b \frac{\mathrm{d}f}{\mathrm{d}x} g \mathrm{d}x \tag{1}$$
関連ページ
高校生向け数学記事の一覧

