積分による円の周・面積、球の表面積・体積の計算

本記事では、積分を用いた円の周・面積、球の表面積・体積に関する関係式（公式）の導出を紹介します。

以下の円の周・面積、球の表面積・体積に関する関係式（公式）は中学校で学びますが、中学校ではこれらの式がどのように導かれるかについてはほとんど学びません。

一般的に、これらの関係式の導出には積分を用いるため、高校数学の知識が必要なりますが、改めてこれらの式の導出過程を確認する高校生は限られていると思います。

本ページでは、積分を用いたEqs. (1~4)の導出過程を紹介します。

円周の関係式（Eq. (1)）の導出

半径\(R\)の円の円周\(l\)の関係式（Eq. (1)）を導きます。

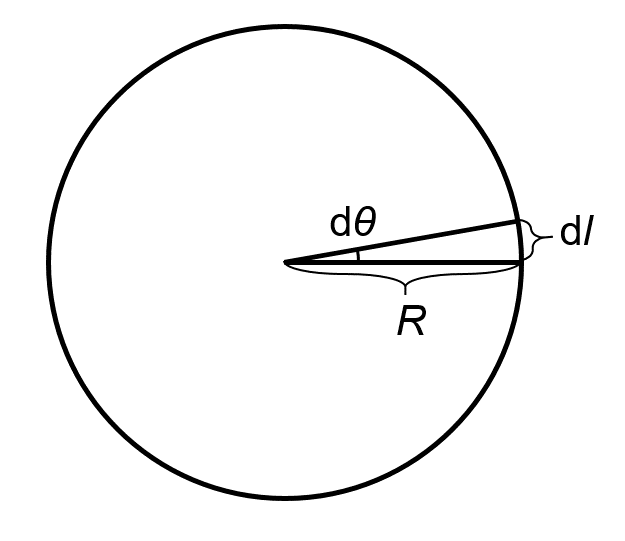
中心角を\(\theta\)として、下図のように微小角\(\mathrm{d} \theta\)が作る微小な弧の長さ\(\mathrm{d}l\)について考えると、その積分によって\(l\)が得られます。

$$ l=\int \mathrm{d}l \tag{1-1}$$

上式は積分区間を記載しておりませんが、不定積分ではなく円周上の全積分です。

ここで、この円が直交座標座標x-yが作る平面上に存在するとすると、以下の方程式が成立します。

$$ x^2+y^2=R^2 \tag{1-2}$$

$$ \mathrm{d}l=\sqrt{\mathrm{d}x^2+\mathrm{d}y^2} \tag{1-3}$$

極座標系を考えると以下の媒介変数表示が成立します。

$$ x=r \cos \theta \tag{1-4}$$

$$ y=r \sin \theta \tag{1-5}$$

円周を考えているので、\(r\)については以下のように一定値になります。

$$ r=R=\mathrm{Const.} \tag{1-6} $$

Eqs. (1-4, 1-5)の\(\theta\)についての微分を考えます。

$$ \frac{\mathrm{d}x}{\mathrm{d} \theta}=-R \sin \theta \tag{1-7} $$

$$ \frac{\mathrm{d}y}{\mathrm{d} \theta}=R \cos \theta \tag{1-8} $$

Eq. (1-1)を変形します。

$$
\begin{eqnarray}
l &=& \int \mathrm{d}l \\
&=& \int \sqrt{\mathrm{d}x^2+\mathrm{d}y^2} \\
&=& \int_0^{2 \pi} \sqrt{ \left( \frac{\mathrm{d}x}{\mathrm{d} \theta} \right) ^2+\left( \frac{\mathrm{d}y}{\mathrm{d} \theta} \right) ^2} \mathrm{d} \theta \\
&=& \int_0^{2 \pi} \sqrt{ \left( -R \sin \theta \right) ^2+\left( R \cos \theta \right) ^2} \mathrm{d} \theta \\
&=& \int_0^{2 \pi} R \sqrt{ \sin ^2 \theta+\cos ^2 \theta} \mathrm{d} \theta \\
&=& R \int_0^{2 \pi} \mathrm{d} \theta \\
&=& R \left[ \theta \right]_0^{2\pi} \\
&=& 2 \pi R \\
\end{eqnarray}
$$

このようにして、Eq. (1)が導かれます。

円の面積（Eq. (2)）の導出

半径\(R\)の円の面積latex]S[/latex]の関係式（Eq. (2)）を導きます。

下図のように、半径\(r\)の円と半径\(r+\mathrm{d}r\)の円に囲まれる微小面積\(\mathrm{d}S\)について考えると、その積分によって\(S\)が得られます。

$$ S=\int \mathrm{d}S \tag{2-1}$$

上式は積分区間を記載しておりませんが、不定積分ではなく円上の全積分です。

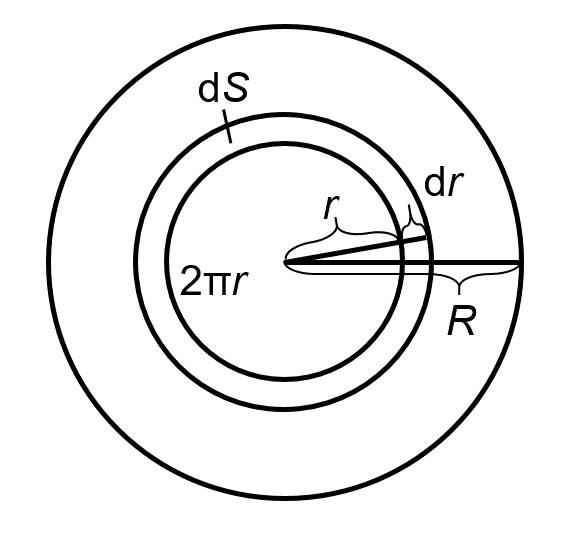
微小面積\(\mathrm{d}S\)は上図から以下の式で与えられます。

$$ \mathrm{d}S=2 \pi r \mathrm{d}r \tag{2-2} $$

Eq. (2-1)を計算します。

$$
\begin{eqnarray}
S &=& \int \mathrm{d}S \\
&=& \int_0^R 2 \pi r \mathrm{d}r \\
&=& 2 \pi \int_0^R r \mathrm{d}r \\
&=& 2 \pi \left[ \frac{1}{2}r^2 \right]_0^R \\
&=& 2 \pi \frac{1}{2}R^2 \\
&=& \pi R^2
\end{eqnarray}
$$

このようにして、Eq. (2)が導かれます。

なお、 Eq. (2-2)の成立には疑問を感じる方もいるかもしれませんが、工学的ではありますが以下のように考えると理解することができます。

$$ 2 \pi r \mathrm{d}r < \mathrm{d}S<2 \pi (r+\mathrm{d}r) \mathrm{d}r $$

$$ \mathrm{Right \quad side} = 2 \pi r \mathrm{d}r +2 \pi \mathrm{d}r ^2 $$

ここで、二次の微小項を無視すると左辺＝右辺となるため挟みうちの原理からEq. (2-2)が成立します。

球の表面積（Eq. (3)）の導出

半径\(R\)の球の表面積\(S\)の関係式（Eq. (3)）を導きます。

下図のように、中心角\(\theta\)、\(\theta +\mathrm{d} \theta\)の球殻上の点の集合で囲まれる微小面積\(\mathrm{d}S\)について考えると、その積分によって\(S\)が得られます。

$$ S=\int \mathrm{d}S \tag{3-1}$$

上式は積分区間を記載しておりませんが、不定積分ではなく球殻上の全積分です。

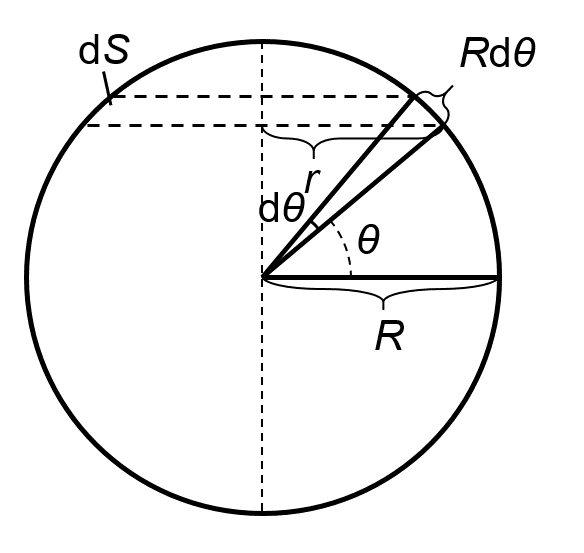
微小面積\(\mathrm{d}S\)は上図から以下の式で与えられます。

$$ \mathrm{d}S=2 \pi r R \mathrm{d} \theta \tag{3-2} $$

ここで、\(r\)は幾何学的な関係から以下の式で与えられます。

$$ r= R \cos \theta \tag{3-3} $$

これらを用いて、Eq. (3-1)を計算します。

$$
\begin{eqnarray}
S &=& \int \mathrm{d}S \\
&=& \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} 2 \pi r R \mathrm{d} \theta \\
&=& 2 \pi R \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} R \cos \theta \mathrm{d} \theta \\
&=& 2 \pi R^2 \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos \theta \mathrm{d} \theta \\
&=& 2 \pi R^2 \left[ \sin \theta \right] _{-\frac{\pi}{2}}^{\frac{\pi}{2}} \\
&=& 2 \pi R^2 \left( 1-(-1) \right) \\
&=& 4 \pi R^2 \\
\end{eqnarray}
$$

このようにして、Eq. (3)が導かれます。

球の体積（Eq. (4)）の導出

半径\(R\)の球の体積\(V\)の関係式（Eq. (4)）を導きます。

下図のように、半径\(r\)の円と半径\(r+\mathrm{d}r\)の球に囲まれる微小体積\(\mathrm{d}V\)について考えると、その積分によって\(V\)が得られます。

$$ V=\int \mathrm{d}V \tag{4-1}$$

上式は積分区間を記載しておりませんが、不定積分ではなく球上の全積分です。

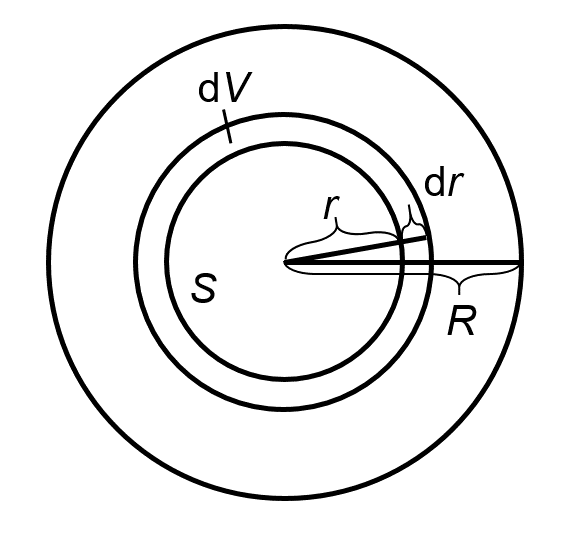
微小面積\(\mathrm{d}V\)は、上図より以下の式で与えられます。

$$ \mathrm{d}V=S \mathrm{d}r \tag{4-2} $$

Eq. (3)を用いて、Eq. (4-1)を計算します。

$$
\begin{eqnarray}
V &=& \int \mathrm{d}V \\
&=& \int_0^R 4 \pi r^2 \mathrm{d}r \\
&=& 4 \pi \int_0^R r^2 \mathrm{d}r \\
&=& 4 \pi \left[ \frac{1}{3}r^3 \right]_0^R \\
&=& \frac{4}{3} \pi R^3 \\
\end{eqnarray}
$$

このようにして、Eq. (4)が導かれます。

---

関連ページ

高校生向け数学記事の一覧