値引きとポイント還元のどちらがお得かを数式で解説

10％の値引きと10％のポイント還元、どちらも割合は同じですが、どちらの方がお得なのでしょうか？

まず、結論をお伝えすると、基本的には値引きの方がお得になります。

本記事では、その理由とそれぞれで得られる利得の差を数式を使って解説します。

また、値引きとポイント還元でお得さが同じになる場合についても解説します。

値引きとポイント還元の数式表現

\(100r\)%の値引きあるいはポイント還元が適用される場合を考えます。

\(C\)円のお金で商品を購入します。

ポイント還元の場合は、得られたポイント分で追加の商品を購入します。ただし、ポイントでの購入分はポイント還元の対象外とします。

入手した商品の総価格を\(P^{\mathrm{all}}\)とし、お得さを評価する指標として\(k\)を下式で定義します。

\[ k=\frac{ P^{\mathrm{all}} }{ C } \tag{1}\]

それでは、値引きとポイント還元それぞれの場合の関係式について説明していきます。

それぞれの場合を区別するため、値引きの場合は下付きのdを、ポイント還元の場合は下付きのpを各変数に付与します。

なお、本稿では、1円未満、1ポイント未満の端数処理は行われないものとし、小数点以下もすべて計算に含めます。

値引きの場合

\( P_{\mathrm{d}}^{\mathrm{all}} \)の商品を購入する場合、\(r_{\mathrm{d}} P_{\mathrm{d}}^{\mathrm{all}}\)が割り引かれるため、支払いに必要な金額は以下のようになります。

\[ C_{\mathrm{d}}= \left( 1-r_{\mathrm{d}} \right) P_{\mathrm{d}}^{\mathrm{all}} \tag{2}\]

これをEq. (1)に代入すると、下式が得られます。

\[ k_{\mathrm{d}}=\frac{P_{\mathrm{d}}^{\mathrm{all}}}{C_{\mathrm{d}}}=\frac{1}{1-r_{\mathrm{d}}} \tag{3}\]

ポイント還元の場合

\(C_{\mathrm{p}}\)の支払いで商品を購入する場合、\((r_{\mathrm{d}} C_{\mathrm{p}}\)のポイントが還元されるため、このポイントでも商品を購入すると、得られる商品総額は以下のようになります。

\[ P_{\mathrm{p}}^{\mathrm{all}} =\left( 1+r_{\mathrm{p}} \right) C_{\mathrm{p}} \tag{4}\]

これをEq. (1)に代入すると、下式が得られます。

\[ k_{\mathrm{p}}=\frac{P_{\mathrm{p}}^{\mathrm{all}}}{C_{\mathrm{p}}}=1+r_{\mathrm{p}} \tag{5}\]

値引きとポイント還元の比較

\(k\)の比較

値引きとポイント還元のお得さを比較するため、\( k_{\mathrm{d}} \)と\( k_{\mathrm{p}} \)を比較してみましょう。

Eqs. (3), (6)をそれぞれ、\(r\)に対してプロットすると、下図のようになります。

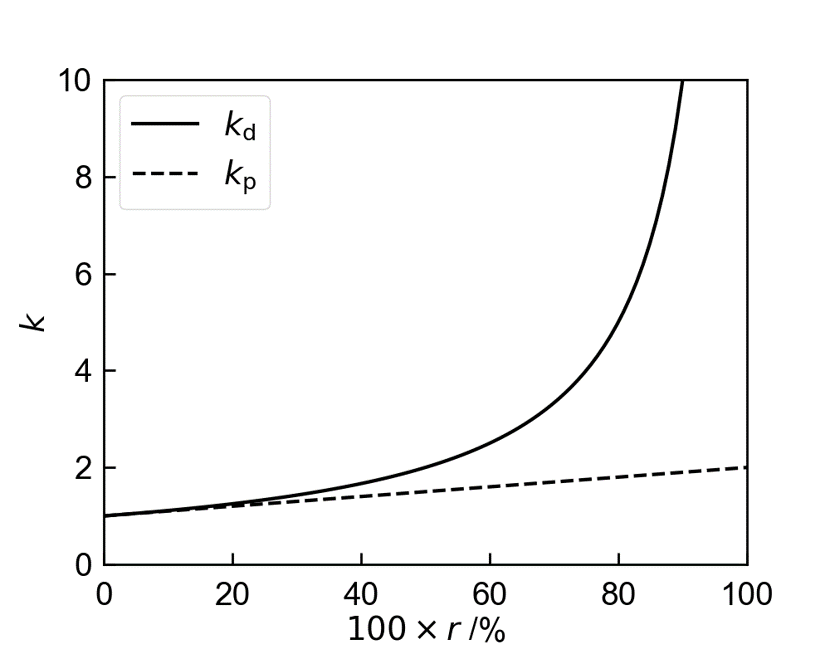
この図から分かるように、\( k_{\mathrm{d}} \geq k_{\mathrm{p}} \)であり、\( r \)が大きくなるにつれ差が大きくなります。

つまり、値引きとポイント還元では値引きの方が得られる利益が大きく、その差は\( r \)が増加するに伴い増大します。

ポイント還元率の換算

上記のように、値引きとポイント還元のどちらがお得かは、\(k\)を計算することで評価できます。

例えば、30%の値引き（\(r_{\mathrm{d}}\)=0.3）と40%のポイント還元（\(r_{\mathrm{p}}\)=0.4）を比較すると、\(k_{\mathrm{d}} \approx 1.43 \)、\(k_{\mathrm{p}}\)=1.40となり、30%の値引きの方がお得なことが分かります。

このように\(k\)を計算することで、\(r\)が異なる場合も、どちらかの方がお得かを知ることができます。

しかし、\(k_{\mathrm{d}} \)と\(k_{\mathrm{p}}\)を両方計算し比較するのは、少し手間がかかり婉曲的です。

そこで、より直接的に両者を比較できるよう、ポイント還元率の換算値\( r_{\mathrm{d \ p}} \)を考えます。

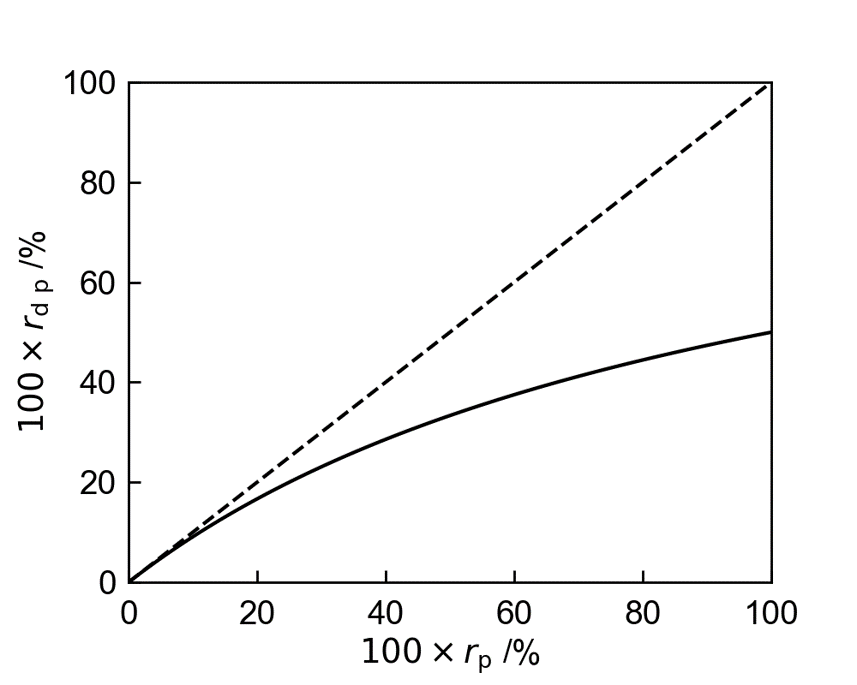
\( r_{\mathrm{d \ p}} \)への換算の考え方は下図の通りです。

\( k_{\mathrm{d}} = k_{\mathrm{p}} \)となるときの、\( r_{\mathrm{d}} \)を\( r_{\mathrm{d / p}} \)とします。

つまり、Eqs. (3), (5)から以下の式が導かれます。

\[ \frac{1}{1-r_{\mathrm{d \ p}}}=1+r_{\mathrm{p}} \]

この式を整理すると、下式が得られます。

\[ r_{\mathrm{d \ p}}=\frac{r_{\mathrm{p}}}{1+r_{\mathrm{p}}} \tag{6} \]

この換算式を用いる事により、より直接的に値引きとポイント還元を比較することができます。

先に挙げた例の場合、40%のポイント還元（\(r_{\mathrm{p}}\)=0.4）では、\(r_{\mathrm{d \ p}} \approx 0.29 \)となるため、30%の値引き（\(r_{\mathrm{d}}\)=0.3）の方がお得であることが分かります。

\(r_{\mathrm{p}} \)と \(r_{\mathrm{d \ p}}\)の比較

いくつかの\(r_{\mathrm{p}} \)について、\(r_{\mathrm{d \ p}} \)を下表に示します。

100\(r_{\mathrm{p}} \) (%)	1%	5%	10%	20%	30%	40%	50%	70%	90%	100%
100\(r_{\mathrm{d \ p}} \) (%)	0.99%	4.8%	9.1%	17%	23%	29%	33%	41%	47%	50%

さらに、\( r_{\mathrm{p}}\)と\( r_{\mathrm{d \ p}}\)の関係を図示すると、以下のようになります。

ポイントでの購入分もポイント還元の対象となる場合

ここまでで、値引きとポイント還元では、値引きの方がお得であることをご理解頂けたかと思います。

では、この差はなぜ生じるのでしょうか？

その原因は、前提条件とした「ポイントでの購入分はポイント還元の対象外」にあります。

それを確認するために、ここでは、ポイントでの購入分もポイントの還元対象をなる場合を考えましょう。

各変数は下付き添え字ppで表現します。

ポイント購入分にも\(r_{\mathrm{pp}}\)を乗じた分のポイントが付与され、ポイントで購入、ポイント付与、再びポイントで購入、さらにポイント付与という操作が無限に繰り返されます。

付与されるポイントは、初項\(C_{\mathrm{pp}} r_{\mathrm{pp}}\)、公比\(r_{\mathrm{pp}}\)の等比数列となるため、\(C_{\mathrm{pp}}\)と\( P_{\mathrm{pp}}^{\mathrm{all}} \)の和となります。

\[ P_{\mathrm{pp}}^{\mathrm{all}}= C_{\mathrm{pp}} + \left\{ \sum_{i=1}^{\infty}C_{\mathrm{pp}} \left( r_{\mathrm{pp}} \right) ^i \right\} \tag{7}\]

これを計算してEq. (1)に代入すると、下式が得られます。

\[ k_{\mathrm{pp}}=\frac{P_{\mathrm{pp}}^{\mathrm{all}}}{C_{\mathrm{pp}}}=\frac{1}{1-r_{\mathrm{pp}}} \tag{8}\]

Eqs. (3), (8)より、\( r_{\mathrm{d}}=r_{\mathrm{pp}}\)のとき、\( k_{\mathrm{d}}=k_{\mathrm{pp}}\)となります。

つまり、ポイントでの購入にもポイントが付与される場合は、値引きとポイント還元のお得さは同じです。

まとめ

・同じ割合の値引きとポイント還元では、基本的に値引きの方がお得である。

・ポイント還元率\(r_{\mathrm{p}}\)は、\(r_{\mathrm{d \ p}}\)に換算することで値引き率\(r_{\mathrm{d}}\)と比較できる。

\[ r_{\mathrm{d \ p}}=\frac{r_{\mathrm{p}}}{1+r_{\mathrm{p}}} \tag{6} \]

・ポイントでの購入分もポイント還元の対象となる場合、値引きとポイント還元のお得さは同じである。

詳細な式展開（PDFファイル）

以下のpdfファイルより、本記事に関係する式展開の詳細をご確認頂けます。

適宜ご参照ください。