本記事では、点と直線の距離の関係式の導出過程を示します。
対象読者:高校生
必要な知識:高校数学 一次関数、ベクトル

点と直線の距離
下図のような点P\(\left( x_0, y_0 \right)\)と直線l: \( ax+by+c=0\)の距離\(d\)は以下の式で与えられます。
$$ d=\frac{\left| a x_0+b y_0+c \right| }{\sqrt{a^2+b^2}} \tag{1}$$
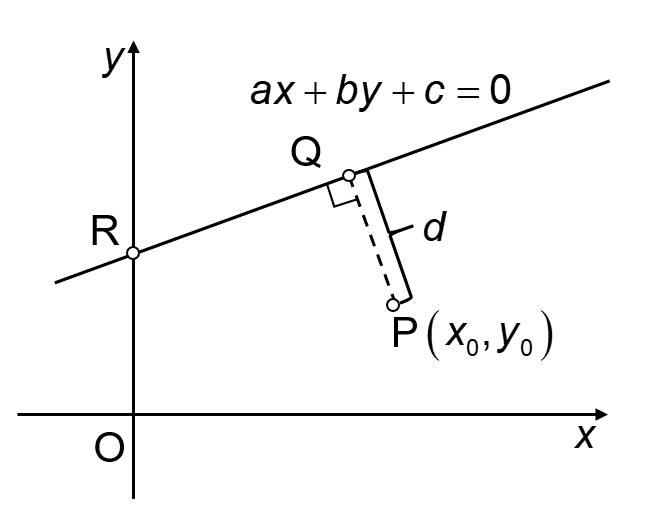
ベクトルを用いた導出
Eq. (1)は以下のよく以下の手順で導かれます。
- 直線lと直交し点Pを通過する直線l’を考え、直線l, l’の連立方程式を解くことで点Qの座標を求めます。
- 点P, Qの座標から線分PQの長さ(\(d\))を求めます。
この手順は計算が煩雑で導出に少し時間が掛かります。
Eq. (1)はベクトルを用いるとシンプルな式で導出できます。本ページでは、ベクトルを用いてEq. (1)を導出します。
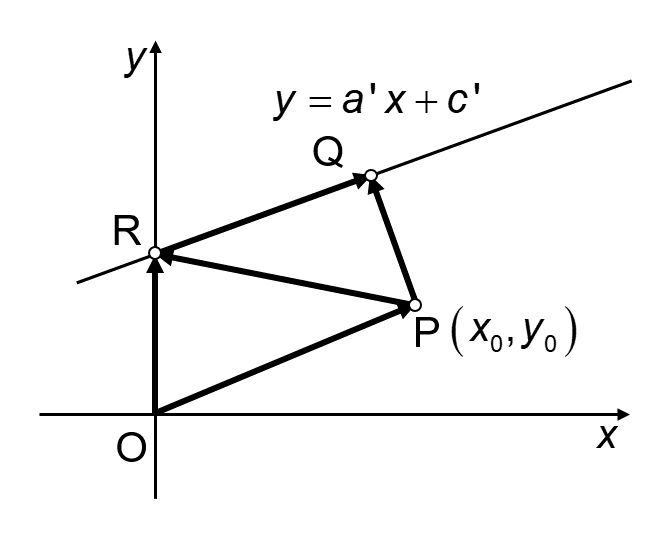
\(b \neq 0 \)として、直線lを以下の形に変形します。
$$ y=a’x+c’ \tag{1-1} $$
$$ a’=-\frac{a}{b} \tag{1-2} $$
$$ c’=-\frac{c}{b} \tag{1-3} $$
\(\vec{\mathrm{RQ}}\)はEq. (1-1)上のベクトルなので、以下の式で表現できます。
$$ \vec{\mathrm{RQ}}=s \left( 1, a’ \right) \tag{1-4} $$
\(\vec{\mathrm{PQ}}\)は\(\vec{\mathrm{RQ}}\)と直交するので、以下の式で表現できます。
\(\vec{\mathrm{PQ}}\)と\(\vec{\mathrm{RQ}}\)の直交
$$ \vec{\mathrm{RQ}} \cdot \vec{\mathrm{PQ}}= 0 \tag{1-5} $$
$$ \vec{\mathrm{PQ}}=t \vec{\mathrm{d’}} \tag{1-6} $$
$$ \vec{\mathrm{d’}}=\left( 1,-\frac{1}{a’} \right) \tag{1-7} $$
Eq. (1-6)を用いると以下の式が成立します。
$$
\begin{eqnarray}
\left| \vec{\mathrm{PQ}} \right| ^2
&=& \left( t \vec{\mathrm{d’}} \right) \cdot \left( t \vec{\mathrm{d’}} \right) \\
&=& t^2 \left| \vec{\mathrm{d’}} \right| ^2 \\
\end{eqnarray}
$$
この式は、Eq. (1-5)と以下の幾何学的な関係式を用いると以下のようにも表現できます。
幾何学的な関係式
$$ \vec{\mathrm{PQ}}=\vec{\mathrm{PR}}+\vec{\mathrm{RQ}} $$
$$
\begin{eqnarray}
\left| \vec{\mathrm{PQ}} \right| ^2
&=& \vec{\mathrm{PQ}} \cdot \left( \vec{\mathrm{PQ}} \right) \\
&=& \vec{\mathrm{PQ}} \cdot \left( \vec{\mathrm{PR}}+\vec{\mathrm{RQ}} \right) \\
&=& \vec{\mathrm{PQ}} \cdot \vec{\mathrm{PR}} + \vec{\mathrm{PQ}} \cdot \vec{\mathrm{RQ}} \\
&=& \vec{\mathrm{PQ}} \cdot \vec{\mathrm{PR}} \\
&=& t\vec{\mathrm{d’}} \cdot \vec{\mathrm{PR}} \\
\end{eqnarray}
$$
\( t \neq 0 \)として、この二つの式から\( t \)を得ます。
$$
\begin{eqnarray}
\left| \vec{\mathrm{PQ}} \right| ^2 = t^2 \left| \vec{\mathrm{d’}} \right| ^2 &=& t\vec{\mathrm{d’}} \cdot \vec{\mathrm{PR}} \\
t \left| \vec{\mathrm{d’}} \right| ^2 &=& \vec{\mathrm{d’}} \cdot \vec{\mathrm{PR}} \\
t &=& \frac{ \vec{\mathrm{d’}} \cdot \vec{\mathrm{PR}} }{ \left| \vec{\mathrm{d’}} \right| ^2 } \\
\end{eqnarray}
$$
ここで、\(d^2\)を考えます。
$$
\begin{eqnarray}
d ^2
&=& \left| \vec{\mathrm{PQ}} \right| ^2 \\
&=& t^2 \left| \vec{\mathrm{d’}} \right| ^2 \\
&=& \left( \frac{ \vec{\mathrm{d’}} \cdot \vec{\mathrm{PR}} }{ \left| \vec{\mathrm{d’}} \right| ^2 } \right)^2 \left| \vec{\mathrm{d’}} \right| ^2 \\
&=& \frac{ \left( \vec{\mathrm{d’}} \cdot \vec{\mathrm{PR}} \right)^2 }{ \left| \vec{\mathrm{d’}} \right| ^2 } \\
\end{eqnarray}
$$
\(d \)は負の数ではないので、以下の式が成立します。
$$ d = \frac{ \left| \vec{\mathrm{d’}} \cdot \vec{\mathrm{PR}} \right| }{ \left| \vec{\mathrm{d’}} \right| } \tag{1-8} $$
Eqs. (1-2, 1-3, 1-7)と以下の関係式を用いると分子の内積は以下のように計算できます。
幾何学的な関係式
$$ \vec{\mathrm{PR}}=-\vec{\mathrm{OP}}+\vec{\mathrm{OR}} $$
ベクトルの成分表示
$$ \vec{\mathrm{OP}}=\left( x_0, y_0 \right) $$
$$ \vec{\mathrm{OR}}=\left( 0, c’ \right) $$
$$
\begin{eqnarray}
\vec{\mathrm{d’}} \cdot \vec{\mathrm{PR}}
&=& \vec{\mathrm{d’}} \cdot \left( -\vec{\mathrm{OP}}+\vec{\mathrm{OR}} \right) \\
&=& – \vec{\mathrm{d’}} \cdot \vec{\mathrm{OP}} + \vec{\mathrm{d’}} \cdot \vec{\mathrm{OR}} \\
&=& – \left( 1, -\frac{1}{a’} \right) \cdot \left( x_0, y_0 \right) + \left( 1, -\frac{1}{a’} \right) \cdot \left( 0, c’ \right) \\
&=& – \left( x_0 -\frac{1}{a’} y_0 \right) + \left( 0 -\frac{1}{a’}c’ \right) \\
&=& – \left( x_0 + \frac{b}{a} y_0 \right) + \left( -\left( -\frac{b}{a} \right) \left( -\frac{c}{b} \right) \right) \\
&=& – \frac{1}{a} \left( a x_0 + b y_0 + c \right) \\
\end{eqnarray}
$$
同様にして、Eqs. (1-2, 1-7)を用いると分母が以下の式で得られます。
$$
\begin{eqnarray}
\left| \vec{\mathrm{d’}} \right|
&=& \sqrt{1+ \left( \frac{1}{a’} \right) ^2 } \\
&=& \sqrt{1+ \left( -\frac{b}{a} \right) ^2 } \\
&=& \sqrt{1+ \frac{b^2}{a^2} } \\
&=& \frac{1}{\sqrt{a^2}} \sqrt{a^2 +b^2 } \\
&=& \frac{1}{\left| a \right|} \sqrt{a^2 +b^2 } \\
\end{eqnarray}
$$
これらの式をEq. (1-8)に代入するとEq. (1)が導かれます。
$$
\begin{eqnarray}
d
&=& \frac{ \left| \vec{\mathrm{d’}} \cdot \vec{\mathrm{PR}} \right| }{ \left| \vec{\mathrm{d’}} \right| } \\
&=& \frac{ \left| – \frac{1}{a} \left( a x_0 + b y_0 + c \right) \right| }{ \frac{1}{\left| a \right|} \sqrt{a^2 +b^2 } } \\
&=& \frac{ \left| \frac{1}{a} \right| \left| \left( a x_0 + b y_0 + c \right) \right| }{ \frac{1}{\left| a \right|} \sqrt{a^2 +b^2 } } \\
&=& \frac{ \left| a x_0 + b y_0 + c \right| }{ \sqrt{a^2 +b^2 } } \\
\end{eqnarray}
$$
\( t = 0 \)の場合を考えると、点Pは直線l上の点となるので、Eq. (1)の右辺は以下のようになるためEq. (1)が成立します。
$$
\begin{eqnarray}
\frac{\left| a x_0+b y_0+c \right| }{\sqrt{a^2+b^2}}
&=& \frac{ 0}{\sqrt{a^2+b^2}} \\
&=& 0 \\
\end{eqnarray}
$$
\(b = 0 \)の場合を考えると、Eq. (1)の右辺は以下の式になります。
$$
\begin{eqnarray}
\frac{\left| a x_0+b y_0+c \right| }{\sqrt{a^2+b^2}}
&=& \frac{\left| ax_0 +c \right| }{\sqrt{a^2}} \\
&=& \frac{\left| a \right| \left| x_0 + \frac{c}{a} \right| }{\left| a \right| } \\
&=& \left| x_0 + \frac{c}{a} \right| \\
\end{eqnarray}
$$
直線lは以下の式になるため、幾何学的な関係からEq. (1)が成立することが確認できます。
直線l
$$ ax+c=0 $$
$$ x=-\frac{c}{a} $$
$$
\begin{eqnarray}
d
&=& \left| x_0 – \left( -\frac{c}{a} \right) \right| \\
&=& \left| x_0 + \frac{c}{a} \right| \\
\end{eqnarray}
$$
これらの事から、Eq. (1)が成立します。
$$ d=\frac{\left| a x_0+b y_0+c \right| }{\sqrt{a^2+b^2}} \tag{1} $$
関連ページ
高校生向け数学記事の一覧

