本記事では、最小二乗法による1変数直線回帰(線形単回帰)について解説します。
\(n\)個のデータ点\(\left\{ \left( x_i , y_i \right) \right\}\)が得られたとき、\(y\)と\(x\)間の関係を解析し、\(y=f(x)\)という関係式を導くのが単回帰分析です。
\(f(x)\)には様々な関数を採用することができ、冪級数がよく用いられます。
冪級数を高次項まで展開するなど、\(f(x)\)には複雑な関数を採用するほどデータ点の再現性は向上しますが、データ点の誤差なども反映してしまい、本質的な関係が見えにくくなることに注意が必要です。
線形単回帰分析は最も基本的な回帰分析であり、\(f(x)=ax+b\)という一次関数に回帰します。
\(a, b\)は定数であり、データ点\(\left\{ \left( x_i , y_i \right) \right\}\)を再現できるように決定する必要があります。
\(a, b\)を決定する方法の一つが最小二乗法です。本記事では最小二乗法を用いた線形単回帰分析についてその関係式を説明します。
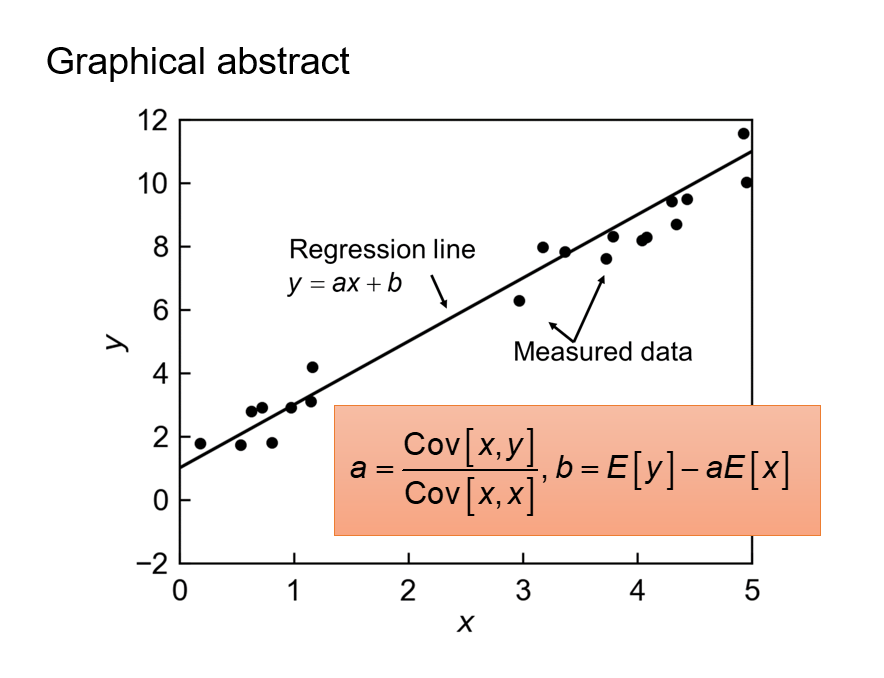
Webページでは要点となる式のみを表示いたしますので、詳細な導出過程については本ページ下部のpdfファイルを参照してください。
最小二乗法
最小二乗法では、データ点\(\left\{ y_i \right\}\)と回帰曲線\(f(x)\)から推定した\(f(x_i)\)の誤差\(I\)を以下の式(二乗誤差)で評価し、この二乗誤差を最小化するように回帰曲線の定数を決定します。
$$ I=\left( y_i – f(x_i) \right)^2 $$
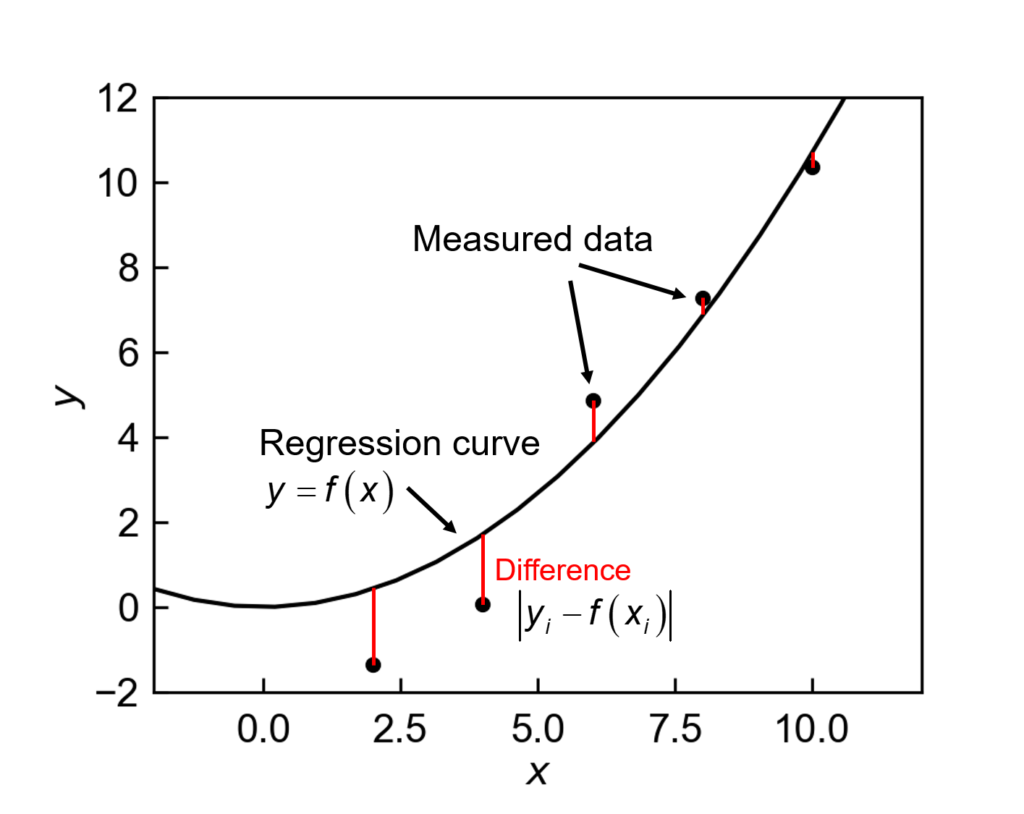
最小二乗法による線形単回帰
回帰式の関数形
線形単回帰分析では、以下のような一次関数に回帰します。
$$ y=f(x)=ax+b \tag{1} $$
ここで、\(a, b\)は定数であり、二乗誤差\(I\)が最小になるように\(a, b\)を決定します。
二乗誤差
二乗誤差\(I\)は\(a, b\)に依存する量であり、以下の式で表現されます。
$$ I(a, b)=\sum_i \left( y_i- \left( ax_i+b \right) \right) ^2 \tag{2} $$
回帰直線
\(I\)を最小化するために以下の方程式を考えます。
$$ \frac{\partial I}{\partial a}=\frac{\partial I}{\partial b}=0 \tag{3} $$
この式を解くことで、\(a, b\)を求めることができます。
詳細な計算過程については本ページ下部のpdfファイルを確認してください。
行列表記
Eq. (3)から以下の式が得られます。
$$
\left[
\begin{array}{c}
a \\ b \\
\end{array}
\right]
=
\left[
\begin{array}{cc}
E[x^2] & E[x] \\
E[x] & 1 \\
\end{array}
\right] ^{-1}
\left[
\begin{array}{cc}
E[xy] \\ E[y] \\
\end{array}
\right]
\tag{4}
$$
\(a, b\)の計算結果
Eq. (4)を計算すると、\(a, b\)は以下のようになります。
$$
a=\frac{\mathrm{Cov}[x,y]}{ \mathrm{Cov}[x,x]} \tag{5}
$$
$$
b=E[y] – \frac{\mathrm{Cov}[x,y]}{ \mathrm{Cov}[x,x]} E [x] = E[y] – aE [x] \tag{6}
$$
回帰直線
Eqs. (5, 6)をEq. (1)に代入することで、回帰直線は以下のようになります。
$$
y=f(x)= \frac{\mathrm{Cov}[x,y]}{ \mathrm{Cov}[x,x]} \left( x-E[x] \right) +E[y] \tag{7}
$$
関係式
Eqs. (5~7)において、\(E [x], \mathrm{Cov} [x,y]\)は、\(\left\{ x_i \right\}\)の平均と\(\left\{ \left( x_i , y_i \right) \right\}\)の共分散であり、以下の式で定義されます。
平均・分散・共分散について、より詳しく知りたい方は以下のページを参照してください。

平均
$$
E [x]=\frac{1}{n} \sum_i x_i \tag{1-1}
$$
分散・共分散
$$
\mathrm{Cov}[x,y]=E \left[ \left( x-E[x] \right) \left( y-E[y] \right) \right] \tag{1-2}
$$
相関係数を用いた表現
相関係数と標準偏差
\(\left\{ \left( x_i , y_i \right) \right\}\)の相関係数\(\rho_{\mathrm{xy}}\)、\(\left\{ x_i \right\}\)の標準偏差\(\sigma_{\mathrm{x}}\)は以下の式で表現されます。
相関係数
$$ \rho_{\mathrm{xy}}=\frac{\mathrm{Cov} \left[ x,y \right]}{\sqrt{\mathrm{Cov} \left[ x,x \right]}\sqrt{\mathrm{Cov} \left[ y,y \right]}} \tag{2-1} $$
標準偏差
$$ \sigma_{\mathrm{x}}= \sqrt{\mathrm{Cov} \left[ x,x \right]} \tag{2-2} $$
定数\(a\)
Eq. (5)はEqs. (2-1, 2-2)を用いると以下のように表現できます。
$$ a= \rho_{\mathrm{xy}} \frac{\sigma_{\mathrm{y}}}{\sigma_{\mathrm{x}}}\tag{2-3} $$
正規化による単回帰直線の変化
以下のように \(\left\{ \left( x_i , y_i \right) \right\}\)を \(\left\{ \left( X_i , Y_i \right) \right\}\)に正規化した場合を考え、正規化による単回帰直線の係数の変化について示します。
詳細な導出過程は本ページ下部のpdfファイルを確認してください。
正規化
\(\left\{ \left( X_i , Y_i \right) \right\}\)は、以下の式で正規化します。
$$ X_i=k \left( x_i -p\right) \tag{3-1} $$
$$ Y_i=l \left( y_i -q\right) \tag{3-2} $$
ここで、\(k, l, p, q\)は任意の定数です。
回帰直線
\(\left\{ \left( X_i , Y_i \right) \right\}\)について、以下の単回帰直線を求めます。
$$ Y=a’X+b’ \tag{3-3} $$
ここで、\(a’, b’\)は定数です。
回帰直線の係数
Eqs. (5, 6)と同様に、最小二乗法によって\(a’, b’\)を求めると以下の関係式が得られます。
$$ a’= \frac{l}{k}a \tag{3-4} $$
$$ b’= l \left\{ b-(q- ap) \right\} \tag{3-5} $$
詳細な式展開(pdfファイル)
各関係式の詳細な導出過程
関連ページ
最小二乗法による線形重回帰(多変数線形回帰)
\(y\)が複数の変数に依存する場合の、最小二乗法による線形回帰については、以下の記事をご確認ください。

最小二乗法による定数への回帰と平均

