本記事では、結晶構造の対称性に由来した、六方晶系の弾性スティフネスの対称性について解説します。
はじめに
弾性スティフネス\(C_{ijkl}\)は4階のテンソルで、添え字の\(i, j, k\)は座標軸を表す1~3の値をとります。
\(C_{ijkl}\)は、結晶構造によらず下式の対称性を有し、独立な21個の成分を持ちます。
\[ C_{ijkl}=C_{jikl}=C_{ijlk}=C_{klij} \tag{1} \]

結晶材料では、それぞれの結晶構造の対称性に基づき、ここからさらに独立成分の数が減少します。
本稿では、六方晶系について、結晶構造の対称性と弾性スティフネスの対称性の関係を解説します。
直方晶・正方晶・立方晶・弾性定数の弾性スティフネスについては、こちらをご覧ください。
本稿では、特に断らない限り、Einstein(アインシュタイン)の総和規約を用いて式を表現します。
下式のように、同一項内に同じ記号の添え字が複数ある場合は、その記号について総和をとる点にご注意ください。
\[ a_i b_i c_j=\sum_i a_i b_i c_j \]
本稿では、\(C_{ijkl}\)を、Vogit表記を用いて、6×6の行列として表記します。

専門:材料力学、弾性論
数学:テンソル
六方晶
六方晶は、直方晶と同様に、任意の\(x_i\)軸の反転に対して不変です。
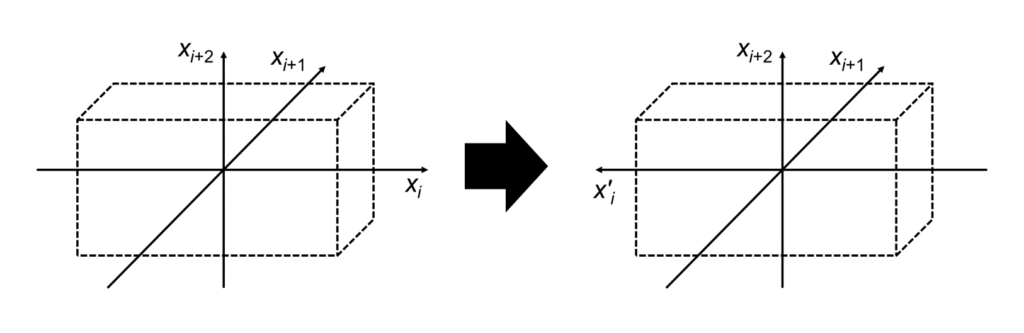

よって、上図のような、\(x_i\)軸の反転を考えると、直方晶と同様に\(C_{ijkl}\)の独立成分数は9つとなり下式が成立します(\(x’_i\)軸は反転後の軸)。
\[
\begin{eqnarray}
\mathbf{C}
&=&
\left[
\begin{array}{cccccc}
C_{11} & C_{12} & C_{31} & & & \\
C_{12} & C_{22} & C_{23} & & \mathrm{O} & \\
C_{31} & C_{23} & C_{33} & & & \\
& & & C_{44} & 0 & 0 \\
& \mathrm{O} & & 0 & C_{55} & 0 \\
& & & 0 & 0 & C_{66} \\
\end{array}
\right]
\end{eqnarray}
\tag{2}
\]
さらに、六方晶は、60°の回転に対して不変であるため、下図のような回転を考えます(\(x’_1\), \(x’_2\)は回転後の軸)。
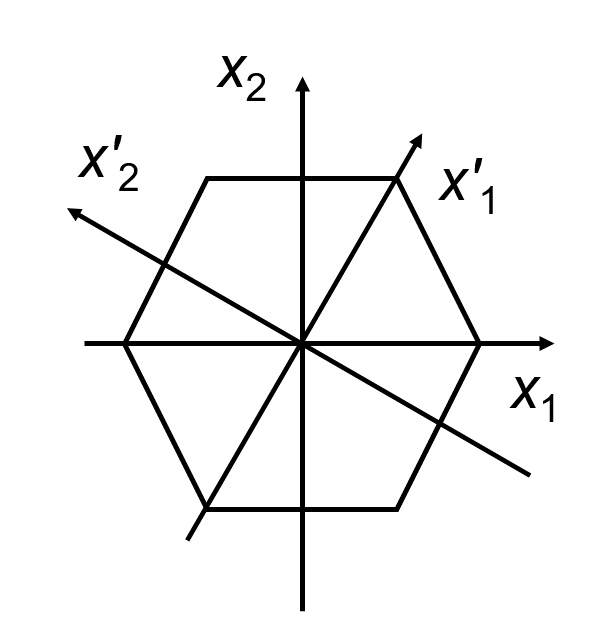
弾性スティフネスの座標変換は下式で表現できます。
\[ C’_{ijkl}=C_{mnpq} l_{im} l_{jn} l_{kp} l_{lq} \tag{3} \]
\[ l_{ij}=\mathbf{e}’_i \cdot \mathbf{e}_j \tag{4} \]
ここで、\(C’_{ijkl}\)は変換後の座標における弾性定数、\(\mathbf{e}’_i\)は変換後の座標における\(x’_i\)軸の単位方向ベクトル、\(\mathbf{e}_i\)は変換前の座標における\(x_i\)軸の単位方向ベクトルです。
上述の座標回転による、\(l_{ij}\)は以下の式で与えられます。
\[
l_{11}=\cos \frac{\pi}{3}=\frac{1}{2} \\
l_{12}=\sin \frac{\pi}{3}=\frac{\sqrt{3}}{2} \\
l_{21}=-\sin \frac{\pi}{3}=-\frac{\sqrt{3}}{2} \\
l_{22}=\cos \frac{\pi}{3}=\frac{1}{2} \\
l_{33}=1 \\
\mathrm{Others}=0\\
\tag{5}
\]
前述の通り、この座標変換に対して、\(C_{ijkl}\)は不変なので、下式が成立します。
\[ C_{ijkl}=C’_{ijkl}=C_{mnpq} l_{im} l_{jn} l_{kp} l_{lq} \tag{6} \]
Eq. (5)を用いて、Eq. (6)と解くと、下式が得られます。
\[ C_{11}=C_{22} \tag{7} \]
\[ C_{66}=\frac{C_{11}-C_{12}}{2} \tag{8} \]
\[ C_{31}=C_{23} \tag{9} \]
\[ C_{55}=C_{44} \tag{10} \]
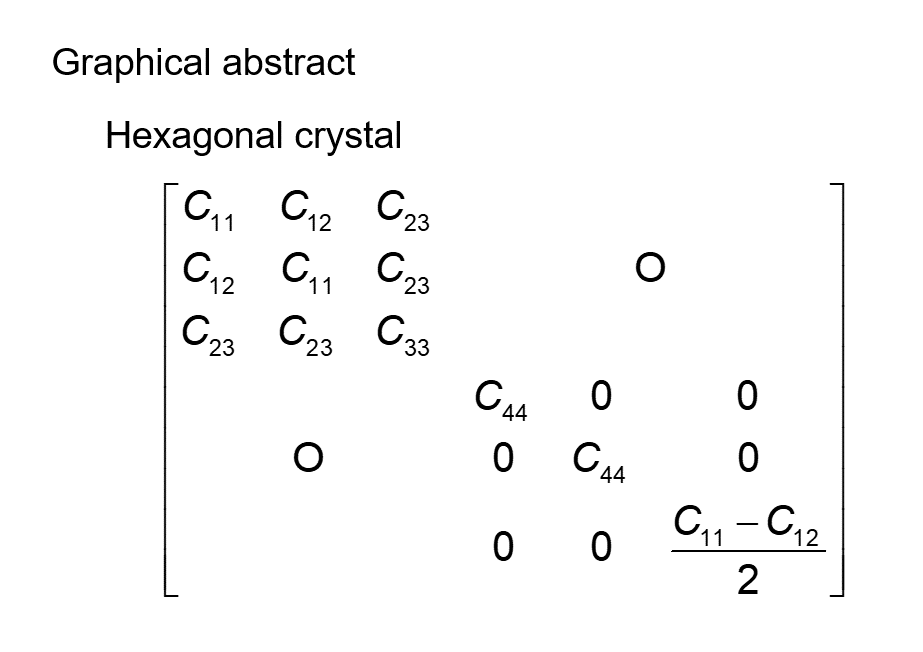
vogit表記を用いると、六方晶の弾性スティフネスは以下の式で与えられます。
\[
\begin{eqnarray}
\mathbf{C}
&=&
\left[
\begin{array}{cccccc}
C_{11} & C_{12} & C_{23} & & & \\
C_{12} & C_{11} & C_{23} & & \mathrm{O} & \\
C_{23} & C_{23} & C_{33} & & & \\
& & & C_{44} & 0 & 0 \\
& \mathrm{O} & & 0 & C_{44} & 0 \\
& & & 0 & 0 & \frac{C_{11}-C_{12}}{2} \\
\end{array}
\right]
\end{eqnarray}
\tag{11} \]
詳細な式展開(PDFファイル)
以下のpdfファイルより、本記事に関係する式展開の詳細をご確認頂けます。
適宜ご参照ください。
