本記事では、結晶系によらずに成立する、弾性スティフネスの対称性について解説します。
はじめに
弾性スティフネスは、\(C_{ijkl}\)と表現される4階のテンソルで、添え字の\(i, j, k\)は座標軸を表す1~3の値をとるため、3×3×3×3の計81個の成分を有します。
本稿では、結晶系によらずに成立する、弾性スティフネスの対称性に関する関係式について、導出過程を解説します。
この関係式は、以下の項目を考えることで導くことができます。
- 応力とひずみの対称性
- 弾性ひずみエネルギーの微分
それぞれの項目について、順に解説していきます。
本稿では、特に断らない限り、Einstein(アインシュタイン)の総和規約を用いて式を表現します。
下式のように、同一項内に同じ記号の添え字が複数ある場合は、その記号について総和をとる点にご注意ください。
\[ a_i b_i c_j=\sum_i a_i b_i c_j \]
専門:材料力学、弾性論
数学:テンソル
応力とひずみの対称性
まず、応力\(\sigma_{ij}\)とひずみ\(\varepsilon_{ij}\)の対称性を考えます。
\[ \sigma_{ij} =\sigma_{ji} \tag{1} \]
\[ \varepsilon_{ij} =\varepsilon_{ji} \tag{2} \]
応力\(\sigma_{ij}\)と、ひずみ\(\varepsilon_{kl}\)の間には、以下のHooke(フック)の法則が成立します。
\[ \sigma_{ij}=C_{ijkl} \varepsilon_{kl} \tag{3} \]
Eq. (3)は、1つの応力成分が9つのひずみ成分の線形結合によって記述できることを表しています。
しかし、Eq. (2)より、ひずみの独立成分は6個であるため、本来、応力成分が6つのひずみ成分の線形結合で十分に記述できるはずです。
さらに、Eq. (1)より、応力の独立成分も6個であるため、本来、Hookeの法則は下式のように、36成分の\(A_{IJKL}\)で十分に記述できるはずです。
\[ \sigma_{IJ}=A_{IJKL} \varepsilon_{KL} \tag{4} \]
ここで、\(I\), \(J\), \(K\), \(L\)は1~3の値をとり、かつ、\(I \leq J\), \(K \leq L\)を満たします。
この\(A_{IJKL}\)は対称性が低いため、対称性を高めるため\(A_{IJKL}\)を拡張したのが、\(C_{ijkl}\)です。
前述の通り、\(A_{IJKL}\)は36成分、\(C_{ijkl}\)は81成分であるため、\(A_{IJKL}\)から\(C_{ijkl}\)を全て決定することはできません。
そこで、\(C_{ijkl}\)に任意性がある場合には、対称性が高くなるように\(C_{ijkl}\)を決定します。
では、\(C_{ijkl}\)の任意性を明確化するため、\(A_{IJKL}\)と\(C_{ijkl}\)の関係式を導きます。
- Eq. (3)
-
\[ \sigma_{IJ}=C_{IJkl} \varepsilon_{kl} \]
- \(k\)と\( l\)の大小関係で和を分割
-
\[ \sigma_{IJ}=C_{IJKL} \varepsilon_{KL}+\left( 1-\delta_{KL} \right)C_{IJLK} \varepsilon_{LK} \]
ここで、\(\delta_{ij}\)はKronecker(クロネッカー)のデルタです。
- Eq. (2)を代入
-
\[ \sigma_{IJ}=\left\{ C_{IJKL} +\left( 1-\delta_{KL} \right)C_{IJLK} \right\} \varepsilon_{KL} \]
- Eq. (4)と比較
-
\[ A_{IJKL} \varepsilon_{KL}=\left\{ C_{IJKL} +\left( 1-\delta_{KL} \right)C_{IJLK} \right\} \varepsilon_{KL} \]
上式は、任意の\(\varepsilon_{KL}\)に対して成立するので、係数を比較すると、下式が得られます。
\[ A_{IJKL} =C_{IJKL} +\left( 1-\delta_{KL} \right)C_{IJLK} \tag{5} \]
また、\(\sigma_{JI}\)についても、Eq. (1)を用いて同様に展開すると、下式が得られます。
\[ A_{IJKL} =C_{JIKL} +\left( 1-\delta_{KL} \right)C_{JILK} \tag{6} \]
これらの関係式から、\(C_{IJKL}\)と\(C_{IJLK}\)、\(C_{JIKL}\)と\(C_{JILK}\)の間に任意性があることが分かりますので、対称性を考慮し以下の関係式を導入します。
\[ C_{IJKL}=C_{IJLK} \]
\[ C_{JIKL}=C_{JILK} \]
これら2式をまとめると、下式が成立します。
\[ C_{ijkl}=C_{ijlk} \tag{7} \]
続いて、Eqs. (5), (6)は左辺が同一なので、右辺同士を比較します。
\[ A_{IJKL} =C_{IJKL} +\left( 1-\delta_{KL} \right)C_{IJLK}C_{JIKL} +\left( 1-\delta_{KL} \right)C_{JILK} \]
Eq. (7)を代入して整理すると、下式が得られます。
\[ C_{IJKL}=C_{JIKL}=C_{IJLK}=C_{JILK} \]
よって、下式が成立します。
\[ C_{ijkl}=C_{jikl} \tag{8} \]
この、Eqs. (8), (9)が応力とひずみの対称性から導入される、\(C_{ijkl}\)の対称性です。
これらの式により、\(C_{ijkl}\)の独立成分数は36となります。
弾性ひずみエネルギーの微分
続いて、単位体積当たりの弾性ひずみエネルギー\(E_{\mathrm{str}}\)の微分について考えます。
\(E_{\mathrm{str}}\)は以下の式で記述されます。
\[ E_{\mathrm{str}}=\frac{1}{2}\sigma_{ij}\varepsilon_{ij} = \frac{1}{2}C_{ijkl}\varepsilon_{ij}\varepsilon_{kl} \tag{9} \]
\(E_{\mathrm{str}}\)はHelmholtz(ヘルムホルツ)エネルギーなので、均一変形を考えると熱力学的共役変数とHelmholtzエネルギーの微分の関係より下式が成立します。
\[ \frac{\partial E_{\mathrm{str}}}{\partial \varepsilon_{ij}}=\sigma_{ij} \tag{10} \]
Eqs. (9), (10)を整理します。
- Eq. (9)を偏微分
-
\[ \frac{\partial E_{\mathrm{str}}}{\partial \varepsilon_{ij}}=\frac{1}{2}\left( C_{ijkl}+C_{klij} \right) \varepsilon_{kl} \]
- Eq. (10)に代入
-
\[ \frac{1}{2}\left( C_{ijkl}+C_{klij} \right) \varepsilon_{kl}=\sigma_{ij} \]
- Hookeの法則(Eq. (3))を代入
-
\[ \frac{1}{2}\left( C_{ijkl}+C_{klij} \right) \varepsilon_{kl}=C_{ijkl} \varepsilon_{kl} \]
- 式を整理
-
\[ C_{klij} \varepsilon_{kl}=C_{ijkl} \varepsilon_{kl} \]
- \(K\), \(L\)を使用して記述
-
\[ C_{KLij} \varepsilon_{KL}+\left( 1-\delta_{KL} \right)C_{LKij} \varepsilon_{LK}=C_{ijKL} \varepsilon_{KL} + \left( 1-\delta_{KL} \right)C_{ijLK} \varepsilon_{LK}\]
- Eqs. (1), (7), (8)を用いて整理
-
\[ \left( 2-\delta_{KL} \right)C_{KLij} \varepsilon_{KL}= \left( 2-\delta_{KL} \right)C_{ijKL} \varepsilon_{KL}\]
この式は、任意の\(\varepsilon_{KL}\)に対して成立するので、係数を比較すると下式が得られます。
\[ C_{KLij} =C_{ijKL} \]
さらに、Eqs. (7), (8)を用いることで、下式が得られます。
\[ C_{ijkl} =C_{klij} \tag{11} \]
まとめ
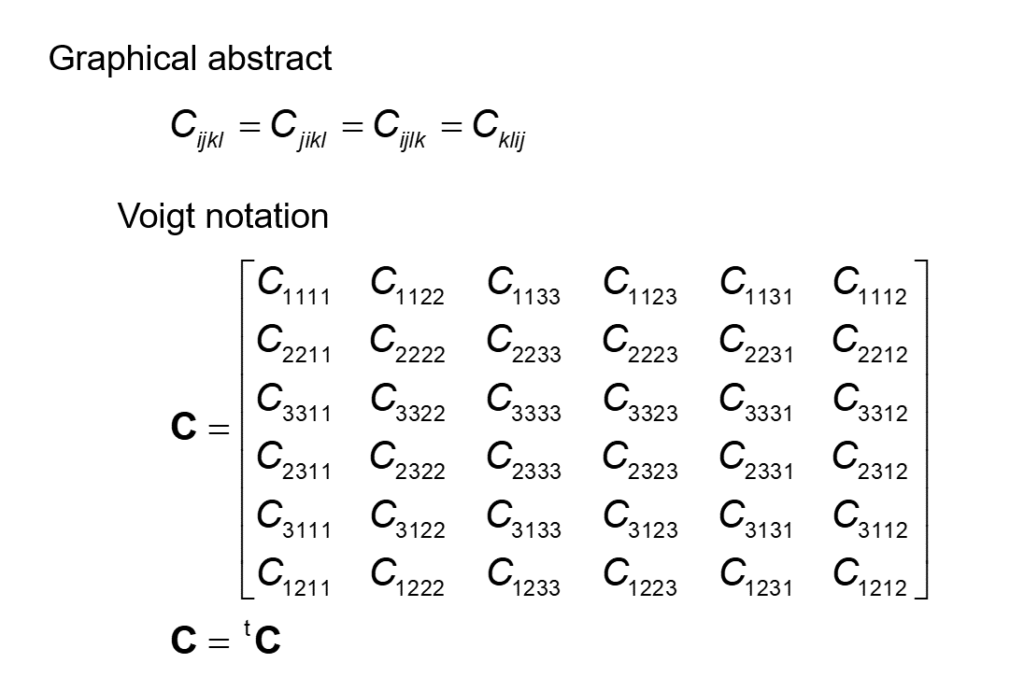
Eqs. (7), (8), (11)をまとめると基本的な対称性として、下式が成立します。
\[ C_{ijkl} =C_{jikl}=C_{ijlk}=C_{klij} \tag{12} \]
この対称性により、\(C_{ijkl}\)の独立な成分は、21個となります。
金属材料では、それぞれの結晶構造の対称性により、さらに独立成分数が減少します。
各結晶構造の弾性スティフネスについては、以下をご確認ください。
詳細な式展開(PDFファイル)
以下のpdfファイルより、本記事に関係する式展開の詳細をご確認頂けます。
適宜ご参照ください。
