本記事では、A-B二元系合金の二相平衡の条件式(共通接線則)を、濃度と相分率を変数として導く方法を紹介します。
共通接線則の導出に関しては、すでに以下の記事で紹介しております。この記事で導く関係式は以下の記事で導いたものと同じです。以下の記事では物質量を変数として共通接線則を導きましたが、本記事では濃度と相分率を変数として共通接線則を導きます(別パターンの導出です)。

Webページ上では要点のみを示しますので、細かな式展開については本ページ下部のpdfファイルをご確認ください。
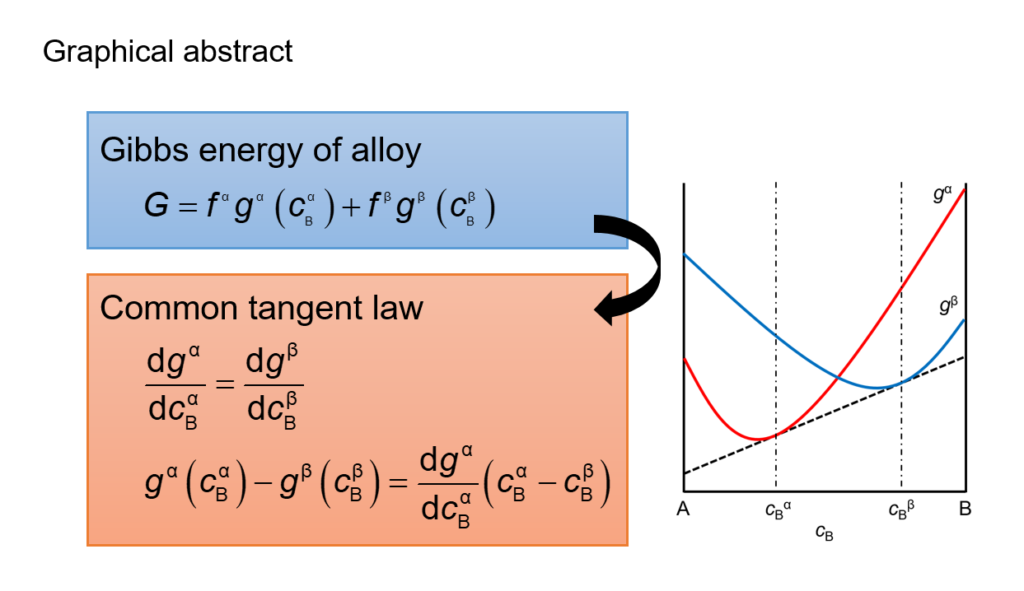
共通接線則
A-B二元系合金において\(\mathrm{\alpha }\)相と\(\mathrm{\beta}\)相の二相が存在している場合を考えます。
系のギブスエネルギー
この系の単位物質量あたりのギブスエネルギー\(G\)は以下の式で与えられます。
$$
G={{f}^{\alpha}}{{g}^{\alpha}}\left( c_{\text{B}}^{\alpha} \right)+{{f}^{\beta}}{{g}^{\beta}}\left( c_{\text{B}}^{\beta} \right) \tag{1-1}
$$
ここで、\(c_{X} ^{P}\)は相\(P\)中の成分\(X\)の濃度、\(g ^P\)は単位物質量当たりの相\(P\)のギブスエネルギー、\(f^P\)は相\(P\)の相分率です。
導出に用いる関係式
二相平衡の条件式は、以下の条件下で\(G\)の最小化を考える事で得ることができます。
$$
f^{\mathrm{\alpha}} +f^{\mathrm{\beta}}=1 \tag{1-2}
$$
$$
c^P _{\mathrm{A}} +c^P _{\mathrm{B}} =1 \tag{1-3}
$$
$$
f^{\mathrm{\alpha}} c^{\mathrm{\alpha}}_X +f^{\mathrm{\beta}} c^{\mathrm{\beta}}_X =c_X =\mathrm{Const.} \tag{1-4}
$$
最小化と極小化は異なる概念ですが、実世界では多くの場合、極小値のいずれかが最小値に一致します。そこで、平衡条件の導出では\(G\)の極小化条件を求めます。
二相平衡の条件式
極小化条件を解くと、二相平衡の条件式(Eqs. (1-5, 1-6))が得られます。
計算手順の詳細は当ページ下部のpdfファイルをご確認ください。
$$
\frac{\text{d}{{g}^{\alpha}}}{\text{d}c_{\text{B}}^{\alpha}}=\frac{\text{d}{{g}^{\beta}}}{\text{d}c_{\text{B}}^{\beta}} \tag{1-5}
$$
$$
{{g}^{\alpha}}-{{g}^{\beta}}=\frac{\text{d}{{g}^{\alpha}}}{\text{d}c_{\text{B}}^{\alpha}}\left( c_{\text{B}}^{\alpha}-c_{\text{B}}^{\beta} \right) \tag{1-6}
$$
詳細な式展開(PDFファイル)
共通接線則の導出(濃度と相分率から定式化)
関連資料
物質量を用いた共通接線則の導出
共通接線則の別パターンの導出を以下のページで紹介しております。
なぜ共通接線則と呼ばれているかについても、以下のページのpdfファイルで紹介しております。

