本記事では、三角関数の加法定理の導出過程を示します。
対象読者:高校生
必要な知識:高校数学 三角関数、ベクトル
三角関数の加法定理
$$ \sin \left( \alpha + \beta \right) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \tag{1}$$
$$ \sin \left( \alpha – \beta \right) = \sin \alpha \cos \beta – \cos \alpha \sin \beta \tag{2}$$
$$ \cos \left( \alpha + \beta \right) = \cos \alpha \cos \beta – \sin \alpha \sin \beta \tag{3}$$
$$ \cos \left( \alpha – \beta \right) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \tag{4}$$
Eqs. (1, 3)の導出
三角関数の加法定理は、よく複数の三角形の幾何学的な関係から説明されていますが、この方法では作図を行う都合、任意の角度\( \alpha, \beta\)について議論することは困難です。
ここでは、単位円と単位円上のベクトルを考えることで、任意の角度について三角関数の加法定理を導きます。
下図のような単位円と単位円上のベクトルを考えます。
(注)ここでは、ベクトルを太字で表します。(例:\( \vec{a}=\mathbf{a} \))
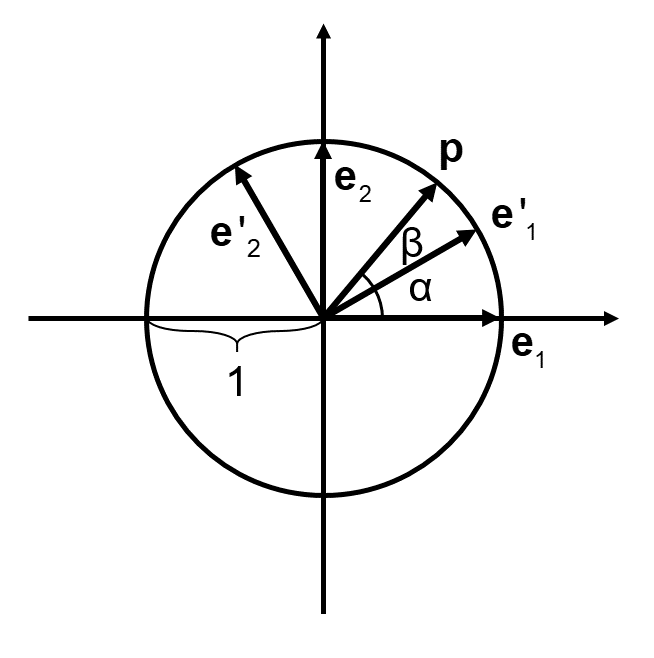
\( \mathbf{e}_2, \mathbf{e}’_2 \)は\( \mathbf{e}_1, \mathbf{e}’_1 \)に直交する単位ベクトルです。上図の関係から、\( \mathbf{e}’_1, \mathbf{e}’_2 \)は\( \mathbf{e}_1, \mathbf{e}_2 \)を用いて、以下の式で与えられます。
$$ \mathbf{e}’_1= \cos \alpha \mathbf{e}_1+ \sin \alpha \mathbf{e}_2 \tag{1-1} $$
$$ \mathbf{e}’_2= -\sin \alpha \mathbf{e}_1+ \cos \alpha \mathbf{e}_2 \tag{1-2} $$
\( \mathbf{p} \)は、\( \mathbf{e}_1, \mathbf{e}_2 \)を用いて表現すると以下のように表現できます。
$$ \mathbf{p}= \cos \left( \alpha + \beta \right) \mathbf{e}_1+ \sin \left( \alpha + \beta \right) \mathbf{e}_2 \tag{1-3} $$
また、\( \mathbf{p} \)は、\( \mathbf{e}’_1, \mathbf{e}’_2 \)を用いて表現すると以下のようになります。
$$ \mathbf{p}= \cos \beta \mathbf{e}’_1+ \sin \beta \mathbf{e}’_2 \tag{1-4} $$
Eq. (1-4)にEqs. (1-1~1-2)を代入します。
$$
\begin{eqnarray}
\mathbf{p}
&=& \cos \beta \mathbf{e}’_1+ \sin \beta \mathbf{e}’_2 \\
&=& \cos \beta \left( \cos \alpha \mathbf{e}_1+ \sin \alpha \mathbf{e}_2 \right) \\
&& + \sin \beta \left( -\sin \alpha \mathbf{e}_1+ \cos \alpha \mathbf{e}_2 \right) \\
&=& \cos \beta \cos \alpha \mathbf{e}_1 + \cos \beta \sin \alpha \mathbf{e}_2 \\
&& – \sin \beta \sin \alpha \mathbf{e}_1 + \sin \beta \cos \alpha \mathbf{e}_2 \\
&=& \left( \cos \alpha \cos \beta – \sin \alpha \sin \beta \right) \mathbf{e}_1 \\
&& + \left( \sin \alpha \cos \beta + \cos \alpha \sin \beta \right) \mathbf{e}_2 \\
\end{eqnarray}
$$
\( \mathbf{e}_1, \mathbf{e}_2 \)は一次独立なので、Eq. (1-3)と係数を比較するとEqs. (1, 3)が導かれます。
$$ \sin \left( \alpha + \beta \right) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \tag{1}$$
$$ \cos \left( \alpha + \beta \right) = \cos \alpha \cos \beta – \sin \alpha \sin \beta \tag{3}$$
Eqs. (2, 4)の導出
Eqs. (1, 3)を用いると以下の式が成立します。
$$
\begin{eqnarray}
\sin \left( \alpha – \beta \right)
&=& \sin \left( \alpha + \left( – \beta \right) \right) \\
&=& \sin \alpha \cos \left( – \beta \right) + \cos \alpha \sin \left( – \beta \right) \\
\end{eqnarray}
$$
$$
\begin{eqnarray}
\cos \left( \alpha – \beta \right)
&=& \cos \left( \alpha + \left( – \beta \right) \right) \\
&=& \cos \alpha \cos \left( – \beta \right) – \sin \alpha \sin \left( – \beta \right) \\
\end{eqnarray}
$$
三角関数の関係式を用いると、Eqs. (2, 4)が導かれます。
三角関数の関係式
$$ \sin \left( – \theta \right) = – \sin \theta \tag{2-1}$$
$$ \cos \left( – \theta \right) = \cos \theta \tag{2-2}$$
$$
\begin{eqnarray}
\sin \left( \alpha – \beta \right)
&=& \sin \alpha \cos \left( – \beta \right) + \cos \alpha \sin \left( – \beta \right) \\
&=& \sin \alpha \cos \beta – \cos \alpha \sin \beta \\
\end{eqnarray}
$$
$$
\begin{eqnarray}
\cos \left( \alpha – \beta \right)
&=& \cos \alpha \cos \left( – \beta \right) – \sin \alpha \sin \left( – \beta \right) \\
&=& \cos \alpha \cos \beta + \sin \alpha \sin \beta \\
\end{eqnarray}
$$
$$ \sin \left( \alpha – \beta \right) = \sin \alpha \cos \beta – \cos \alpha \sin \beta \tag{2}$$
$$ \cos \left( \alpha – \beta \right) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \tag{4}$$
関連ページ
高校生向け数学記事の一覧

