最小二乗法による定数への回帰と平均値

2022年2月9日

本記事では、最小二乗法による定数への回帰と平均値の関係について解説します。

以下の記事では、最も基本的な回帰分析である最小二乗法による線形単回帰分析について解説しました。

あわせて読みたい

最小二乗法による線形単回帰（1変数直線回帰）本記事では、最小二乗法による1変数直線回帰（線形単回帰）について解説します。個のデータ点が得られたとき、と間の関係を解析し、という関係式を導くのが単回帰分析...

線形単回帰よりも簡単な回帰には定数への回帰があります。本記事で紹介するように、最小二乗法による定数への回帰は平均値に一致します。それゆえに、最小二乗法による定数への回帰を意識的に考えることはほとんどありませんが、平均値をとれば二乗誤差が最小化されているということを理解しておくことは有益です。

Webページでは要点となる式のみを表示いたしますので、詳細な導出過程については本ページ下部のpdfファイルを参照してください。

最小二乗法による定数への回帰

$n$個のデータ点$\left\{ y_i \right\}$を最小二乗法により定数$b$に回帰します。

二乗誤差$I$は以下の式で評価します。

$$ I(b)=\sum_i \left( y_i- b \right) ^2 \tag{1} $$

Eq. (1)を整理すると、以下の二次関数が得られます。

詳細な計算過程については本ページ下部のpdfファイルを確認してください。

$$ I(b)=n \left( \left( b- E\left[ y \right] \right) ^2 +\mathrm{Cov}\left[ y,y \right] \right) \tag{2} $$

この式は下図のように下に凸の二次関数なので、$I$を最小化する$b$は以下の式で与えられます。

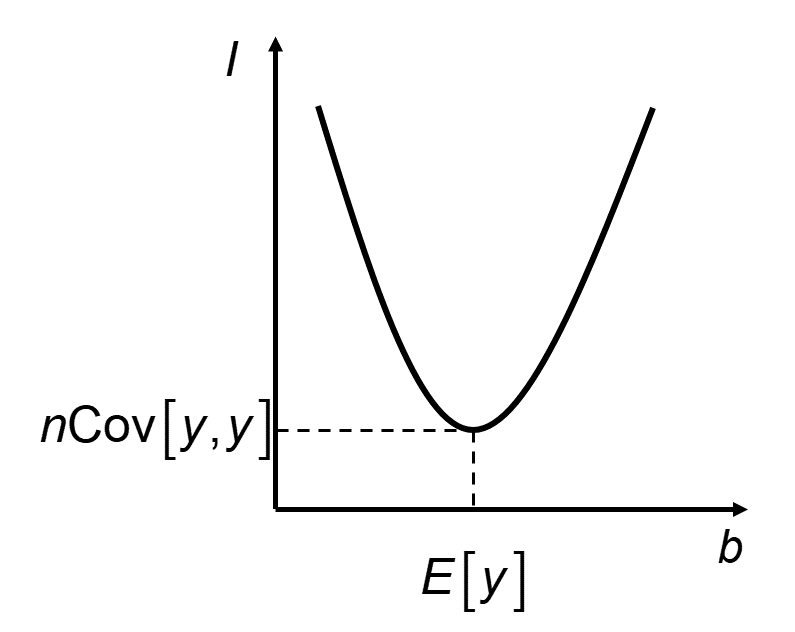
$$ b=E\left[ y \right] \tag{3} $$

$$ \mathrm{min} \left( I(b) \right)=n \mathrm{Cov}\left[ y,y \right] \tag{4} $$

ここで、$E [x], \mathrm{Cov} [y,y]$は、$\left\{ x_i \right\}$の平均と分散です。

平均・分散・共分散について、より詳しく知りたい方は以下のページを参照してください。

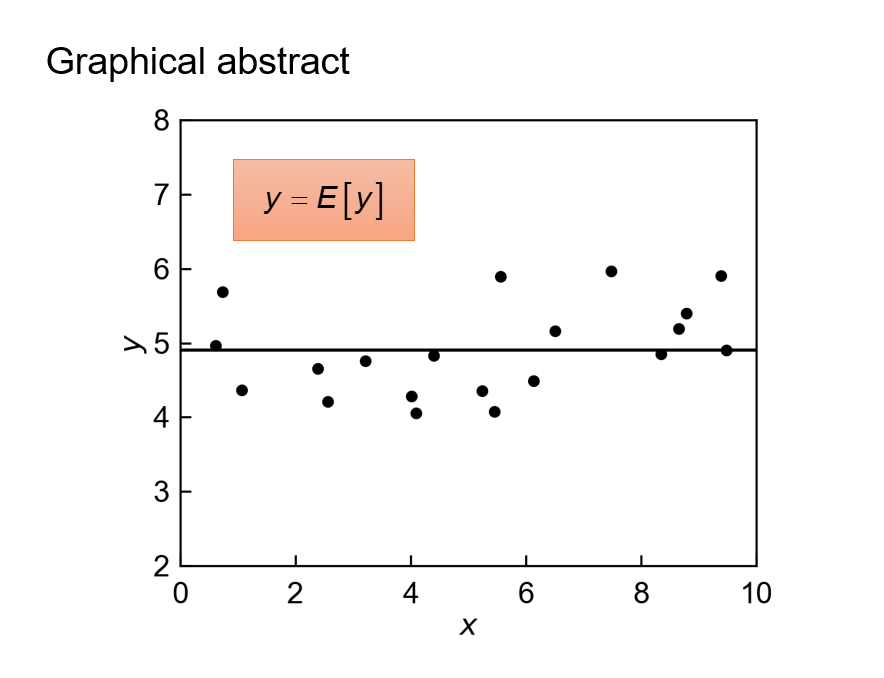
Eq. (3)より、最小二乗法で定数へ回帰すると定数は$\left\{ y_i \right\}$の平均値に一致します。

また、この時の二乗誤差はEq. (4)に示したように$\left\{ y_i \right\}$の分散の$n$倍に一致します。

つまり、$\left\{ y_i \right\}$の平均値をとることは、$\left\{ y_i \right\}$を最小二乗法により定数に回帰することと等しく、その平均二乗誤差は$\left\{ y_i \right\}$の分散により求めることができます。